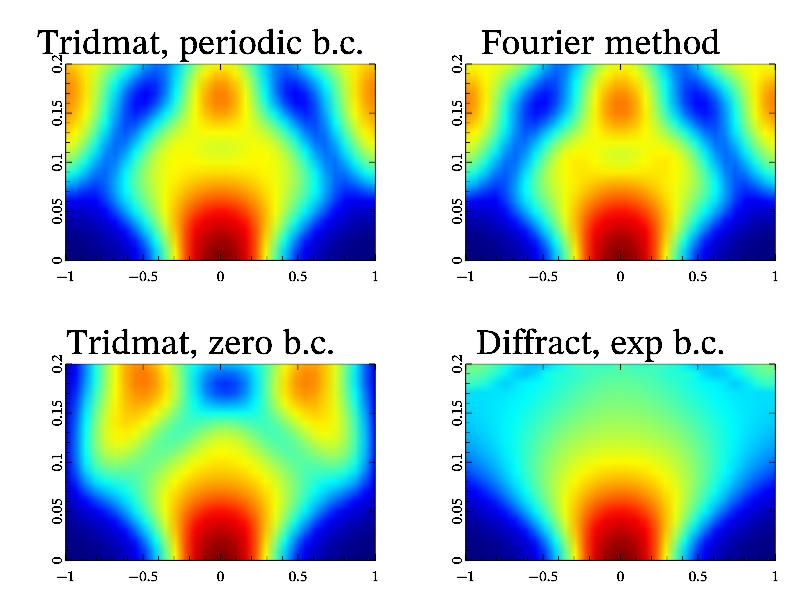
11.47 Sample ‘diffract’ ¶
MGL code:
define n 32 #number of points define m 20 # number of iterations define dt 0.01 # time step new res n m+1 ranges -1 1 0 m*dt 0 1 #tridmat periodic variant new !a n 'i',dt*(n/2)^2/2 copy !b !(1-2*a) new !u n 'exp(-6*x^2)' put res u all 0 for $i 0 m tridmat u a b a u 'xdc' put res u all $i+1 next subplot 2 2 0 '<_':title 'Tridmat, periodic b.c.' axis:box:dens res #fourier variant new k n:fillsample k 'xk' copy !e !exp(-i1*dt*k^2) new !u n 'exp(-6*x^2)' put res u all 0 for $i 0 m fourier u 'x' multo u e fourier u 'ix' put res u all $i+1 next subplot 2 2 1 '<_':title 'Fourier method' axis:box:dens res #tridmat zero variant new !u n 'exp(-6*x^2)' put res u all 0 for $i 0 m tridmat u a b a u 'xd' put res u all $i+1 next subplot 2 2 2 '<_':title 'Tridmat, zero b.c.' axis:box:dens res #diffract exp variant new !u n 'exp(-6*x^2)' define q dt*(n/2)^2/8 # need q<0.4 !!! put res u all 0 for $i 0 m for $j 1 8 # due to smaller dt diffract u 'xe' q next put res u all $i+1 next subplot 2 2 3 '<_':title 'Diffract, exp b.c.' axis:box:dens res
C++ code:
void smgl_diffract(mglGraph *gr)
{
long n=32; // number of points
long m=20; // number of iterations
double dt=0.01; // time step
mglData res(n,m+1);
gr->SetRanges(-1,1, 0,m*dt, 0,1);
// tridmat periodic variant
mglDataC a(n), b(n); a = dual(0,dt*n*n/8);
for(long i=0;i<n;i++) b.a[i] = mreal(1)-mreal(2)*a.a[i];
mglDataC u(n); gr->Fill(u,"exp(-6*x^2)"); res.Put(u,-1,0);
for(long i=0;i<m;i++)
{
u = mglTridMatC(a,b,a,u,"xdc");
res.Put(u,-1,i+1);
}
gr->SubPlot(2,2,0,"<_"); gr->Title("Tridmat, periodic b.c.");
gr->Axis(); gr->Box(); gr->Dens(res);
// fourier variant
mglData k(n); k.FillSample("xk");
mglDataC e(n); for(long i=0;i<n;i++) e.a[i] = exp(-dual(0,dt*k.a[i]*k.a[i]));
gr->Fill(u,"exp(-6*x^2)"); res.Put(u,-1,0);
for(long i=0;i<m;i++)
{
u.FFT("x"); u *= e; u.FFT("ix");
res.Put(u,-1,i+1);
}
gr->SubPlot(2,2,1,"<_"); gr->Title("Fourier method");
gr->Axis(); gr->Box(); gr->Dens(res);
// tridmat zero variant
gr->Fill(u,"exp(-6*x^2)"); res.Put(u,-1,0);
for(long i=0;i<m;i++)
{
u = mglTridMatC(a,b,a,u,"xd");
res.Put(u,-1,i+1);
}
gr->SubPlot(2,2,2,"<_"); gr->Title("Tridmat, zero b.c.");
gr->Axis(); gr->Box(); gr->Dens(res);
// diffract exp variant
gr->Fill(u,"exp(-6*x^2)"); res.Put(u,-1,0);
double q=dt*n*n/4/8; // NOTE: need q<0.4 !!!
for(long i=0;i<m;i++)
{
for(long j=0;j<8;j++) // due to smaller dt
u.Diffraction("xe",q);
res.Put(u,-1,i+1);
}
gr->SubPlot(2,2,3,"<_"); gr->Title("Diffract, exp b.c.");
gr->Axis(); gr->Box(); gr->Dens(res);
}