---

3.2.6 Ternary axis ¶

There are another unusual axis types which are supported by MathGL. These are ternary and quaternary axis. Ternary axis is special axis of 3 coordinates a, b, c which satisfy relation a+b+c=1. Correspondingly, quaternary axis is special axis of 4 coordinates a, b, c, d which satisfy relation a+b+c+d=1.

Generally speaking, only 2 of coordinates (3 for quaternary) are independent. So, MathGL just introduce some special transformation formulas which treat a as ‘x’, b as ‘y’ (and c as ‘z’ for quaternary). As result, all plotting functions (curves, surfaces, contours and so on) work as usual, but in new axis. You should use ternary function for switching to ternary/quaternary coordinates. The sample code is:

int sample(mglGraph *gr)
{
  gr->SetRanges(0,1,0,1,0,1);
  mglData x(50),y(50),z(50),rx(10),ry(10), a(20,30);
  a.Modify("30*x*y*(1-x-y)^2*(x+y<1)");
  x.Modify("0.25*(1+cos(2*pi*x))");
  y.Modify("0.25*(1+sin(2*pi*x))");
  rx.Modify("rnd"); ry.Modify("(1-v)*rnd",rx);
  z.Modify("x");

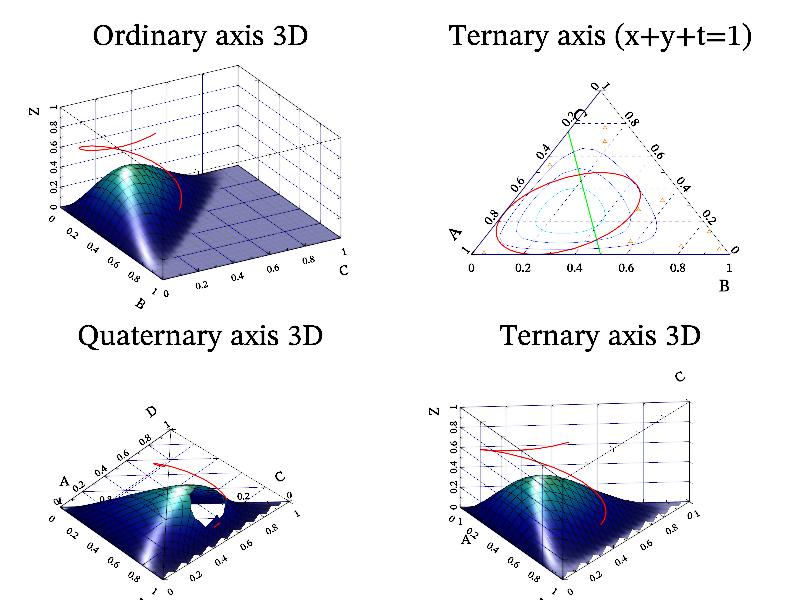
  gr->SubPlot(2,2,0); gr->Title("Ordinary axis 3D");
  gr->Rotate(50,60);    gr->Light(true);
  gr->Plot(x,y,z,"r2"); gr->Surf(a,"BbcyrR#");
  gr->Axis(); gr->Grid(); gr->Box();
  gr->Label('x',"B",1); gr->Label('y',"C",1); gr->Label('z',"Z",1);

  gr->SubPlot(2,2,1); gr->Title("Ternary axis (x+y+t=1)");
  gr->Ternary(1);
  gr->Plot(x,y,"r2"); gr->Plot(rx,ry,"q^ ");  gr->Cont(a,"BbcyrR");
  gr->Line(mglPoint(0.5,0), mglPoint(0,0.75), "g2");
  gr->Axis(); gr->Grid("xyz","B;");
  gr->Label('x',"B"); gr->Label('y',"C"); gr->Label('t',"A");

  gr->SubPlot(2,2,2); gr->Title("Quaternary axis 3D");
  gr->Rotate(50,60);    gr->Light(true);
  gr->Ternary(2);
  gr->Plot(x,y,z,"r2"); gr->Surf(a,"BbcyrR#");
  gr->Axis(); gr->Grid(); gr->Box();
  gr->Label('t',"A",1); gr->Label('x',"B",1);
  gr->Label('y',"C",1); gr->Label('z',"D",1);

  gr->SubPlot(2,2,3); gr->Title("Ternary axis 3D");
  gr->Rotate(50,60);    gr->Light(true);
  gr->Ternary(1);
  gr->Plot(x,y,z,"r2"); gr->Surf(a,"BbcyrR#");
  gr->Axis(); gr->Grid(); gr->Box();
  gr->Label('t',"A",1); gr->Label('x',"B",1);
  gr->Label('y',"C",1); gr->Label('z',"Z",1);
  return 0;
}