11.102 Sample ‘qo2d’ ¶
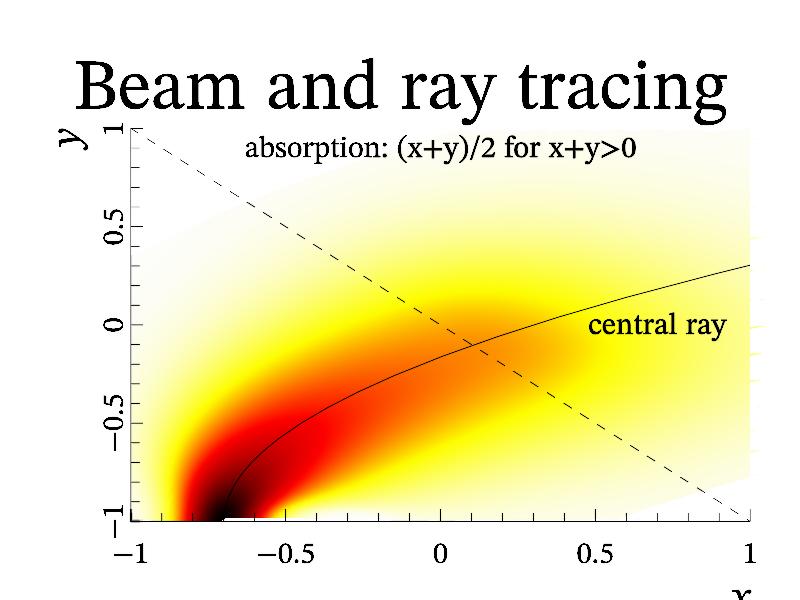
Example of PDE solving by quasioptical approach qo2d.
MGL code:
define $1 'p^2+q^2-x-1+i*0.5*(y+x)*(y>-x)' subplot 1 1 0 '<_':title 'Beam and ray tracing' ray r $1 -0.7 -1 0 0 0.5 0 0.02 2:plot r(0) r(1) 'k' axis:xlabel '\i x':ylabel '\i z' new re 128 'exp(-48*x^2)':new im 128 new xx 1:new yy 1 qo2d a $1 re im r 1 30 xx yy crange 0 1:dens xx yy a 'wyrRk':fplot '-x' 'k|' text 0 0.85 'absorption: (x+y)/2 for x+y>0' text 0.7 -0.05 'central ray'
C++ code:
void smgl_qo2d(mglGraph *gr)
{
mglData r, xx, yy, a, im(128), re(128);
const char *ham = "p^2+q^2-x-1+i*0.5*(y+x)*(y>-x)";
r = mglRay(ham, mglPoint(-0.7, -1), mglPoint(0, 0.5), 0.02, 2);
if(big!=3) {gr->SubPlot(1,1,0,"<_"); gr->Title("Beam and ray tracing");}
gr->Plot(r.SubData(0), r.SubData(1), "k");
gr->Axis(); gr->Label('x', "\\i x"); gr->Label('y', "\\i y");
// now start beam tracing
gr->Fill(re,"exp(-48*x^2)");
a = mglQO2d(ham, re, im, r, xx, yy, 1, 30);
gr->SetRange('c',0, 1);
gr->Dens(xx, yy, a, "wyrRk");
gr->FPlot("-x", "k|");
gr->Puts(mglPoint(0, 0.85), "absorption: (x+y)/2 for x+y>0");
gr->Puts(mglPoint(0.7, -0.05), "central ray");
}