| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
MathGL is ...
| 1.1 Why have I written MathGL? | ||
| 1.2 MathGL features | ||
| 1.3 Installation and usage | ||
| 1.4 General concepts | ||
| 1.5 FAQ | ||
| 1.6 Interfaces | ||
| 1.7 Thanks |
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
A code for making high-quality scientific graphics under Linux and Windows. A code for the fast handling and plotting of large data arrays. A code for working in window and console regimes and for easy including into another program. A code with large and renewal set of graphics. Exactly such a code I was looking for in the last years. Exactly such a code I tried to realize in MathGL library.
At this version (1.11.2) MathGL has more than 20000 code strings, more than 40 general types of graphics for 1d, 2d and 3d data arrays. It can export graphics to bitmap and vector (EPS or SVG) files. It has OpenGL interface and can be used from console programs. It has functions for data handling and script MGL language for simplification of data plotting. It also has several types of transparency and smoothed lighting, vector fonts and TeX-like symbol parsing, arbitrary curvilinear coordinate system and many other useful things (see pictures section at homepage). Finally it is platform-independent and free (under GPL v.2.0 or later license).
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
MathGL can plot a wide range of graphics. It includes:
In fact, I created the functions for drawing of all the types of scientific plots that I know. The list of plots is growing; if you need some special type of a plot then please email me e-mail and it will appear in the new version.
I tried to make plots as nice looking as possible: e.g., a surface can be transparent and highlighted by several (up to 10) light sources. Most of the drawing functions have 2 variants: simple one for the fast plotting of data, complex one for specifying of the exact position of the plot (including parametric representation). Resulting image can be saved in bitmap (with the help of mglGraphZB, mglGraphGL) PNG, JPEG, TIFF, BMP format or in vector EPS or SVG format (with the help of mglGraphPS), or in IDTF format (with the help of mglGraphIDTF) which can be converted into U3D.
All texts are drawn by vector fonts, which allows for high scalability and portability. Texts may contain commands for: some of the TeX-like symbols, changing index (upper or lower indexes) and the style of font inside the text string (see section mglFont class). Texts of ticks are rotated with axis rotation. It is possible to create a legend of plot and put text in an arbitrary position on the plot. Arbitrary text encoding (by the help of function setlocale()) and UTF-16 encoding are supported.
Special mglData class is used for data encapsulation (see section mglData class). In addition to a safe creation and deletion of data arrays it includes functions for data processing (smoothing, differentiating, integrating, interpolating and so on) and reading of data files with automatic size determination. Class mglData can handle arrays with up to three dimensions (arrays which depend on up to 3 independent indexes a_ijk). Using an array with higher number of dimensions is not meaningful, because I do not know how it can be plotted. Data filling and modification may be done manually or by textual formulas.
The mglFormula class allows a fast evaluation of a textual mathematical expression (see section mglFormula class). It is based on string precompilation to tree-like code at the creation of class instance. At evaluation stage code performs only fast tree-walk and returns the value of the expression. In addition to changing data values, textual formulas are also used for drawing in arbitrary curvilinear coordinates. A set of such curvilinear coordinates is limited only by user</samp>’s imagination rather than a fixed list like: polar, parabolic, spherical, and so on.
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
MathGL can be installed in 4 different ways.
./configure after it make and make install with root/sudo rights. Sometimes after installation you may need to update the library list – just execute ldconfig with root/sudo rights.
Script ./configure have several additional options which are switched off by default. They are: --enable-fltk, --enable-glut, --enable-qt for ebabling FLTK, GLUT and/or Qt windows; --enable-jpeg, --enable-tiff, --enable-hdf5 for enabling corresponding file formats; --enable-all for enabling all additional features. For using double as base internal data type use option --enable-double. For enabling language interfaces use --enable-python, --enable-octave or --enable-langall for all languages. The full list of options can be viewed by command ./configure --help.
To compile your own program, you need to specify the linker option -lmgl for a compilation in the console program or with external (non-MathGL) window library. If you want to use FLTK or GLUT windows then you need to add the option -lmgl-fltk or -lmgl-glut. Fortran users also should add C++ library by the option -lstdc++.
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
The set of MathGL features is rather rich – just the number of basic graphics types is larger than 40. Also there are functions for data handling, plot setup and so on. In spite of it I tried to keep a similar style in function names and in the order of arguments. Mostly it is used for different drawing functions.
There are six most general (base) concepts:
In addition to the general concepts I want to comment on some non-trivial or less commonly used general ideas – plot positioning, axis specification and curvilinear coordinates, styles for lines, text and color scheme.
| 1.4.1 Coordinate axes | ||
| 1.4.2 Line styles | ||
| 1.4.3 Color scheme | ||
| 1.4.4 Font styles | ||
| 1.4.5 Textual formulas |
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
Two axis representations are used in MathGL. The first one consists of normalizing the data point coordinates in a box MinxMax (see section Axis settings). If Cut is true then the outlier points are omitted, otherwise they are projected to the bounding box (see section Cutting). Also, the point will be omitted if it lies inside the box defined by CutMin x CutMax or if the value of formula CutOff() is nonzero for its coordinates. After that, transformation formulas are applied to the data point. Finally, the data point is plotted by one of the functions.
There is a possibility to set members Max, Min directly, but one should call RecalcBorder() function to setup plotting routines. A safer way is to set these values by calling the Axis() function, which calls RecalcBorder() automatically. Another way to specify the scaling of the axis is to set it as a minimal or maximal value of the data array. Functions XRange(), YRange(), ZRange() do it. The second (optional) argument is used to replace the axis range or to join with the existed range.
The axis origin is defined by the variable Org and is applied to all consequent calls of axes or grid drawing. By default, if this point lies outside the bounding box then it is projected onto the one (variable AutoOrg controls it). If one of the values of Org is equal to NAN then the corresponding value will be selected automatically.
There is 4-th axis c (color axis or colorbar) in addition to the usual axes x, y, z. It sets the range of values for the surface coloring. Its borders are automatically set to values of Min.z, Max.z during the call of Axis() function. Also, one can directly change the color range by setting variables Cmax, Cmax, or calling functions CAxis() or CRange(). Use Colorbar() function for showing the colorbar.
The form (appearence) of tick labels is controlled by SetTicks() function (see section Axis settings). It has 3 arguments: first one d sets the tick step (if positive) or tick number (if negative) or switches logarithmic ticks on (if zero); the second one, ns, sets the number of subticks; the last one is the starting point for ticks (default is axis origin). Function SetTuneTicks switches on/off tick enhancing by factoring out acommon multiplier (for small coordinate values, like 0.001 to 0.002, or large, like from 1000 to 2000) or common component (for narrow range, like from 0.999 to 1.000). Finally, you may use functions SetXTT(), SetYTT(), SetZTT(), SetCTT() for setting templates for tick labels (it supports TeX symbols). Also, there is a possibility to print arbitrary text as tick labels the by help of SetTicksVal() function.
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
The line style is defined by the string which may contain specifications for color (‘wkrgbcymhRGBCYMHWlenupqLENUPQ’), dashing style (‘-|;:ji’ or space), width (‘0123456789’) and marks (‘o+xsd.^v’ and ‘#’ modifier). If one of the type of information is omitted then default values used with the previous color or one from palette (for see section 1D plotting) are adopted. By default palette contain following colors: dark gray ‘H’, blue ‘b’, green ‘g’, red ‘r’, cyan ‘c’, magenta ‘m’, yellow ‘y’, gray ‘h’, green-blue ‘l’, sky-blue ‘n’, orange ‘q’, green-yellow ‘e’, blue-violet ‘u’, purple ‘p’.
The color types are: ‘k’ -- black, ‘r’ -- red, ‘R’ -- dark red, ‘g’ -- green, ‘G’ -- dark green, ‘b’ -- blue, ‘B’ -- dark blue, ‘c’ -- cyan, ‘C’ -- dark cyan, ‘m’ -- magenta, ‘M’ -- dark magenta, ‘y’ -- yellow, ‘Y’ -- dark yellow (gold), ‘h’ -- gray, ‘H’ -- dark gray, ‘w’ -- white, ‘W’ -- bright gray, ‘l’ -- green-blue, ‘L’ -- dark green-blue, ‘e’ -- green-yellow, ‘E’ -- dark green-yellow, ‘n’ -- sky-blue, ‘N’ -- dark sky-blue, ‘u’ -- blue-violet, ‘U’ -- dark blue-violet, ‘p’ -- purple, ‘P’ -- dark purple, ‘q’ -- orange, ‘Q’ -- dark orange (brown).
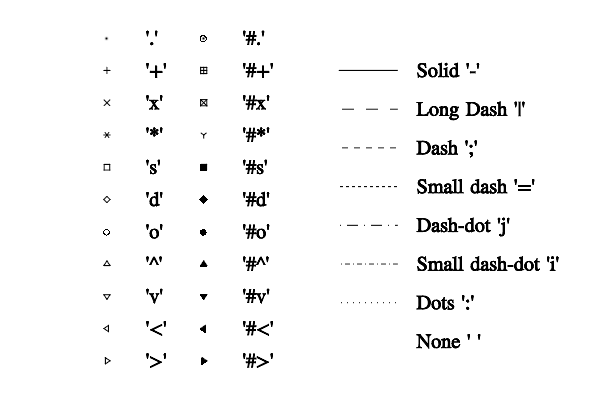
Dashing style has the following meaning: space -- no line (usable for plotting only marks), ‘-’ -- solid line (■■■■■■■■■■■■■■■■), ‘|’ -- long dashed line (■■■■■■■■□□□□□□□□), ‘;’ -- dashed line (■■■■□□□□■■■■□□□□), ‘=’ -- small dashed line (■■□□■■□□■■□□■■□□), ‘:’ -- dotted line (■□□□■□□□■□□□■□□□), ‘j’ -- dash-dotted line (■■■■■■■□□□□■□□□□), ‘i’ -- small dash-dotted line (■■■□□■□□■■■□□■□□).Marker types are: ‘o’ – circle, ‘+’ – cross, ‘x’ – skew cross, ‘s’ - square, ‘d’ - rhomb (or diamond), ‘.’ – dot (point), ‘^’ – triangle up, ‘v’ – triangle down, ‘<’ – triangle left, ‘>’ – triangle right, ‘#*’ – Y sign, ‘#+’ – squared cross, ‘#x’ – squared skew cross, ‘#.’ – circled dot. If string contain symbol ‘#’ then the solid versions of markers are used.

Styles of lines and marks.
One may specify to draw a special symbol (an arrow) at the beginning and at the end of line. This is done if the specification string contains one of the following symbols: ‘A’ – outer arrow, ‘V’ – inner arrow, ‘I’ – transverse hatches, ‘K’ – arrow with hatches, ‘T’ – triangle, ‘S’ – square, ‘D’ – rhombus, ‘O’ – circle, ‘_’ – nothing (the default). The following rule applies: the first symbol specifies the arrow at the end of line, the second specifies the arrow at the beginning of the line. For example, ‘r-A’ defines a red solid line with usual arrow at the end, ‘b|AI’ defines a blue dash line with an arrow at the end and with hatches at the beginning, ‘_O’ defines a line with the current style and with a circle at the beginning. These styles are applicable during the graphics plotting as well (for example, 1D plotting).
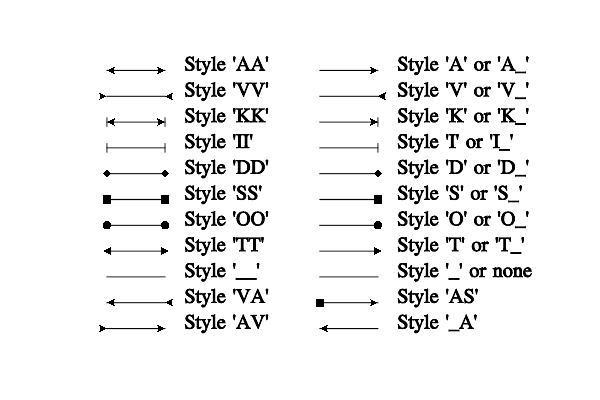
Arrow styles.
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
The color scheme is used for determining the color of surfaces, isolines, isosurfaces and so on. The color scheme is defined by the string, which may contain several characters that are color id (see section Line styles) or characters ‘d#:|’. Symbol ‘d’ denotes the interpolation by 3d position instead of the coloring by amplitude. Symbol ‘#’ switches to mesh drawing or to a wire plot. Symbol ‘|’ disables color interpolation in color scheme, which can be useful, for example, for sharp colors during matrix plotting. Symbol ‘:’ finishes the color scheme parsing. Following it, the user may put styles for the text, rotation axis for curves/isocontours, and so on. Color scheme may contain up to 32 color values.
You may also use “lighted” colors in the color scheme specification (not in line style!). The “lighted” color contain 2 symbols: first one is the usual symbol for color specification, the second one is a digit for its brightness. The digit can be in range ‘1’...‘9’. Number ‘5’ corresponds to a normal color, ‘1’ is a very dark version of the color (practically black), and ‘9’ is a very bright version of the color (practically white). For example, the color scheme can be ‘b2b7wr7r2’.

Colors and its ids.
For coloring by amplitude (most common) the final color is a linear interpolation of color array. The color array is constructed from the string ids. The argument is the amplitude normalized between Cmin – Cmax (see section Axis settings). For example, string containing 4 characters ‘bcyr’ corresponds to a colorbar from blue (lowest value) through cyan (next value) through yellow (next value) to the red (highest value). String ‘kw’ corresponds to a colorbar from black (lowest value) to white (highest value). String ‘m’ corresponds to a simple magenta color.
There are several useful combinations. String ‘kw’ corresponds to the simplest gray color scheme where higher values are brighter. String ‘wk’ presents the inverse gray color scheme where higher value is darker. Strings ‘kRryw’, ‘kGgw’, ‘kBbcw’ present the well-known hot, summer and winter color schemes. Strings ‘BbwrR’ and ‘bBkRr’ allow to view bi-color figure on white or black background, where negative values are blue and positive values are red. String ‘BbcyrR’ gives a color scheme similar to the well-known jet color scheme.

Most popular color schemes.
When coloring by coordinate, the final color is determined by the position of the point in 3d space and is calculated from formula c=x*c[1] + y*c[2] + z*c[3]. Here, c[1], c[2], c[3] are the first three elements of color array; x, y, z are normalized to Min – Max coordinates of the point. This type of coloring is useful for isosurface plot where color may show the exact position of a piece of surface.
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
Text style is specified by the string which may contain several characters of font (‘ribwou’) and/or alignment (‘LRC’) specifications. The string also may contain the color id characters ‘wkrgbcymhRGBCYMHW’ (see section Line styles) after the symbol ‘:’. For example, ‘biC:b’ sets the bold italic font text aligned at the center and with blue color.
The font types are: ‘r’ – roman font, ‘i’ – italic style, ‘b’ – bold style. By default roman roman font is used. The align types are: ‘L’ – align left (default), ‘C’ – align center, ‘R’ – align right. Additional font effects are: ‘w’ – wired, ‘o’ – over-lined, ‘u’ – underlined.
Also a parsing of the LaTeX-like syntax is provided. There are commands for the font style changing inside the string (for example, use \b for bold font): \a or \overline – over-lined, \b or \textbf – bold, \i or \textit – italic, \r or \textrm – roman (disable bold and italic attributes), \u or \underline – underlined, \w or \wire – wired, \big – bigger size, @ – smaller size. The lower and upper indexes are specified by ‘_’ and ‘^’ symbols. At this the changed font style is applied only on next symbol or symbols in braces {}. The text in braces {} are treated as single symbol that allow one to print the index of index. For example, compare the strings ‘sin (x^{2^3})’ and ‘sin (x^2^3)’. You may also change text color inside string by command #? or by \color? where ‘?’ is symbolic id of the color (see section Line styles). For example, words ‘Blue’ and ‘red’ will be colored in the string ‘#b{Blue} and \colorr{red} text’. The most of functions understand the newline symbol ‘\n’ and allows to print multi-line text. Finally, you can use arbitrary UTF codes by command \utf0x????. For example, \utf0x3b1 will produce
α symbol.
The most of commands for special TeX or AMSTeX symbols, the commands for font style changing (\textrm, \textbf, \textit, \textsc, \overline, \underline), accents (\hat, \tilde, \dot, \ddot, \acute, \check, \grave, \bar, \breve) and roots (\sqrt, \sqrt3, \sqrt4) are recognized. The full list contain approximately 2000 commands. Note that first space symbol after the command is ignored, but second one is printed as normal symbol (space). For example, the following strings produce the same result \tilde a: ‘\tilde{a}’; ‘\tilde a’; ‘\tilde{}a’.
In particular, the Greek letters are recognizable special symbols: α – \alpha, β – \beta, γ – \gamma, δ – \delta, ε – \epsilon, η – \eta, ι – \iota, χ – \chi, κ – \kappa, λ – \lambda, μ – \mu, ν – \nu, o – \o, ω – \omega, ϕ – \phi, π – \pi, ψ – \psi, ρ – \rho, σ – \sigma, θ – \theta, τ – \tau, υ – \upsilon, ξ – \xi, ζ – \zeta, ς – \varsigma, ɛ – \varepsilon, ϑ – \vartheta, φ – \varphi, ϰ – \varkappa; A – \Alpha, B – \Beta, Γ – \Gamma, Δ – \Delta, E – \Epsilon, H – \Eta, I – \Iota, C – \Chi, K – \Kappa, Λ – \Lambda, M – \Mu, N – \Nu, O – \O, Ω – \Omega, Φ – \Phi, Π – \Pi, Ψ – \Psi, R – \Rho, Σ – \Sigma, Θ – \Theta, T – \Tau, Υ – \Upsilon, Ξ – \Xi, Z – \Zeta.The small part of most common special TeX symbols are: ∠ – \angle, ⋅ – \cdot, ♣ – \clubsuit, ✓ – \checkmark, ∪ – \cup, ∩ – \cap, ♢ – \diamondsuit, ◇ – \diamond, ÷ – \div, ↓ – \downarrow, † – \dag, ‡ – \ddag, ≡ – \equiv, ∃ – \exists, ⌢ – \frown, ♭ – \flat, ≥ – \ge, ≥ – \geq, ≧ – \geqq, ← – \gets, ♡ – \heartsuit, ∞ – \infty, ∫ – \int, \Int, ℑ – \Im, ♢ – \lozenge, ⟨ – \langle, ≤ – \le, ≤ – \leq, ≦ – \leqq, ← – \leftarrow, ∓ – \mp, ∇ – \nabla, ≠ – \ne, ≠ – \neq, ♮ – \natural, ∮ – \oint, ⊙ – \odot, ⊕ – \oplus, ∂ – \partial, ∥ – \parallel, ⊥ –\perp, ± – \pm, ∝ – \propto, ∏ – \prod, ℜ – \Re, → – \rightarrow, ⟩ – \rangle, ♠ – \spadesuit, ~ – \sim, ⌣ – \smile, ⊂ – \subset, ⊃ – \supset, √ – \sqrt or \surd, § – \S, ♯ – \sharp, ∑ – \sum, × – \times, → – \to, ∴ – \therefore, ↑ – \uparrow, ℘ – \wp.
The font size can be defined explicitly (if size>0) or relative to a base font size as |size|*FontSize (if size<0). The value size=0 specifies that the string will not be printed. The base font size is measured in internal “MathGL” units. Special functions SetFontSizePT(), SetFontSizeCM(), SetFontSizeIN() allow one to set it in more “common” variables for a given dpi value of the picture.
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
MathGL have the fast variant of textual formula evaluation (see section mglFormula class) . There are a lot of functions and operators available. The operators are: ‘+’ – addition, ‘-’ – subtraction, ‘*’ – multiplication, ‘/’ – division, ‘^’ – integer power. Also there are logical “operators”: ‘<’ – true if x<y, ‘>’ – true if x>y, ‘=’ – true if x=y, ‘&’ – true if x and y both nonzero, ‘|’ – true if x or y nonzero. These logical operators have lowest priority and return 1 if true or 0 if false.
The basic functions are: ‘sqrt(x)’ – square root of x, ‘pow(x,y)’ – power x in y, ‘ln(x)’ – natural logarithm of x, ‘lg(x)’ – decimal logarithm of x, ‘log(a,x)’ – logarithm base a of x, ‘abs(x)’ – absolute value of x, ‘sign(x)’ – sign of x, ‘mod(x,y)’ – x modulo y, ‘step(x)’ – step function, ‘int(x)’ – integer part of x, ‘rnd’ – random number, ‘pi’ – number π = 3.1415926…
Trigonometric functions are: ‘sin(x)’, ‘cos(x)’, ‘tan(x)’ (or ‘tg(x)’). Inverse trigonometric functions are: ‘asin(x)’, ‘acos(x)’, ‘atan(x)’. Hyperbolic functions are: ‘sinh(x)’ (or ‘sh(x)’), ‘cosh(x)’ (or ‘ch(x)’), ‘tanh(x)’ (or ‘th(x)’). Inverse hyperbolic functions are: ‘asinh(x)’, ‘acosh(x)’, ‘atanh(x)’.
There are a set of special functions: ‘gamma(x)’ – Gamma function Γ(x) = ∫0∞ tx-1 exp(-t) dt, ‘psi(x)’ – digamma function ψ(x) = Γ′(x)/Γ(x) for x≠0, ‘ai(x)’ – Airy function Ai(x), ‘bi(x)’ – Airy function Bi(x), ‘cl(x)’ – Clausen function, ‘li2(x)’ (or ‘dilog(x)’) – dilogarithm Li2(x) = -ℜ∫0xds log(1-s)/s, ‘sinc(x)’ – compute sinc(x) = sin(πx)/(πx) for any value of x, ‘zeta(x)’ – Riemann zeta function ζ(s) = ∑k=1∞k-s for arbitrary s≠1, ‘eta(x)’ – eta function η(s) = (1 - 21-s)ζ(s) for arbitrary s, ‘lp(l,x)’ – Legendre polynomial Pl(x), (|x|≤1, l≥0), ‘w0(x)’ – principal branch of the Lambert W function, ‘w1(x)’ – principal branch of the Lambert W function. Function W(x) is defined to be solution of the equation: W exp(W) = x.
The exponent integrals are: ‘ci(x)’ – Cosine integral Ci(x) = ∫0xdt cos(t)/t, ‘si(x)’ – Sine integral Si(x) = ∫0xdt sin(t)/t, ‘erf(x)’ – error function erf(x) = (2/√π) ∫0xdt exp(-t2) , ‘ei(x)’ – exponential integral Ei(x) = -PV(∫-x∞dt exp(-t)/t) (where PV denotes the principal value of the integral), ‘e1(x)’ – exponential integral E1(x) = ℜ∫1∞dt exp(-xt)/t, ‘e2(x)’ – exponential integral E2(x) = ℜ∫1∞dt exp(-xt)/t2, ‘ei3(x)’ – exponential integral Ei3(x) = ∫0xdt exp(-t3) for x≥0.
Bessel functions are: ‘j(nu,x)’ – regular cylindrical Bessel function of fractional order nu, ‘y(nu,x)’ – irregular cylindrical Bessel function of fractional order nu, ‘i(nu,x)’ – regular modified Bessel function of fractional order nu, ‘k(nu,x)’ – irregular modified Bessel function of fractional order nu.
Elliptic integrals are: ‘ee(k)’ – complete elliptic integral is denoted by E(k) = E(π/2,k), ‘ek(k)’ – complete elliptic integral is denoted by K(k) = F(π/2,k), ‘e(phi,k)’ – elliptic integral E(φ,k) = ∫0φdt √(1 - k2sin2(t)), ‘f(phi,k)’ – elliptic integral F(φ,k) = ∫0φdt 1/√(1 - k2sin2(t))
Jacobi elliptic functions are: ‘sn(u,m)’, ‘cn(u,m)’, ‘dn(u,m)’, ‘sc(u,m)’, ‘sd(u,m)’, ‘ns(u,m)’, ‘cs(u,m)’, ‘cd(u,m)’, ‘nc(u,m)’, ‘ds(u,m)’, ‘dc(u,m)’, ‘nd(u,m)’.
Note, some of these functions are unavailable if NO_GSL is defined during compilation of MathGL library.
There is no difference between lower or upper case in formulas. If argument value lie outside the range of function definition then function returns NaN.
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
Check that points of the plot lie inside the bounding box and resize the bounding box using Axis() function. Check that the data have correct dimensions for selected type of plot. Be sure that Finish() is called after the plotting functions (or be sure that the plot is saved to a file). Sometimes the light reflection from flat surfaces (like, Dens()) can look as if the plot were absent.
Most “new” types of plots can be created by using the existing drawing functions. For example, the surface of curve rotation can be created by a special function Torus(), or as a parametrically specified surface by Surf(). See also, Hints and MathGL examples of MathGL. If you can not find a specific type of plot, please e-mail me and this plot will appear in the next version of MathGL library.
No. The MathGL library is self-contained and does not require the knowledge of external libraries.
The core of the MathGL library is written in C++. But there are interfaces for: pure C, Fortran, Pascal, Forth, and its own command language MGL. Also there is a large set of interpreted languages, which are supported (Python, Java, ALLEGROCL, CHICKEN, Lisp, CFFI, C#, Guile, Lua, Modula 3, Mzscheme, Ocaml, Octave, Perl, PHP, Pike, R, Ruby, Tcl). These interfaces are written using SWIG (both pure C functions and classes) but only the interface for Python and Octave is included in the autoconf/automake script. The reason is that I don</samp>’t know any other interpreted languages :(. Note that most other languages can use (link to) the pure C functions.
You can use MathGL as is with gfortran because it uses by default the AT&T notation for external functions. For other compilers (like Visual Fortran) you have to switch on the AT&T notation manually. The AT&T notation requires that the symbol ‘_’ is added at the end of each function name, function argument(s) is passed by pointers and the string length(s) is passed at the end of the argument list. For example:
C function – void mgl_fplot(HMGL graph, const char *fy, const char *stl, int n);
AT&T function – void mgl_fplot_(uintptr_t *graph, const char *fy, const char *stl, int *n, int ly, int ls);
The member-functions of classes have a hidden parameter (the pointer to a class instance) in C++. So, their direct usage is impossible. The solution is to write an interface function:
int foo_draw(mglGraph *gr, void *par)
{ ((Foo *)foo)->draw(gr); }
|
and to use it in the call of Window() function:
gr->Window(argc,argv,foo_draw,"Title",this); |
Alternatively you can inherit your class from mglDraw class and use the functions like gr->Window(argc, argv, foo, "Title");.
The standard way is to use Unicode encoding for the text output. But the MathGL library also has interface for 8-bit (char *) strings with internal conversion to Unicode. This conversion depends on the current locale OS. You may change it by setlocale() function. For example, for Russian text in CP1251 encoding you may use setlocale(LC_CTYPE, "ru_RU.cp1251"); (under MS Windows the name of locale may differ – setlocale(LC_CTYPE, "russian_russia.1251")). I strongly recommend not to use the constant LC_ALL in the conversion. Since it also changes the number format, it may lead to mistakes in formula writing and reading of the text in data files. For example, the program will await a ‘,’ as a decimal point but the user will enter ‘.’.
There are 3 general ways. First, the point with NAN value as one of the coordinates will never be plotted. Second, special variables CutMin, CutMax or function CutOff() define the condition when the points should be omitted (see section Cutting). Last, you may change the transparency of a part of the plot by the help of functions SurfA(), Surf3A() (see section Dual plotting). In this last case the transparency is switched on smoothly.
In version 1.10, you can use the header file #include <mgl/mgl_w.h> which contains wrapper C++ classes, which should be acceptable for any compiler. Note, that wrapper classes are incompatible with classes in usual headers and you should use only one of them (wrapper or usual)! However, I recommend to use the usual headers if you use GNU compilers (like MinGW).
The simplest way is using the combination CMake+MinGW. Also you need some extra libraries like GSL, PNG, JPEG and so on. All of them can be found at http://gnuwin32.sourceforge.net/packages.html. After installing all components, just run CMake configurator and make the MathGL itself.
You should create a separate thread for processing window messages. The cross-platform way is using the pthread library. You can update the data by calling mglGraphFLTK::Update() function. The code can look like this:
//-----------------------------------------------------------------------------
#include <mgl/mgl_fltk.h>
#include <pthread.h>
#include <unistd.h>
mglPoint pnt; // some global variable for changable data
//-----------------------------------------------------------------------------
int sample(mglGraph *gr, void *)
{
gr->Box(); gr->Line(mglPoint(),pnt,"Ar2"); // just draw a vector
return 0;
}
//-----------------------------------------------------------------------------
void *mgl_fltk_tmp(void *) { mglFlRun(); return 0; }
int main (int argc, char ** argv)
{
mglGraphFLTK gr;
gr.Window(argc,argv,sample,"test"); // create window
static pthread_t tmp;
pthread_create(&tmp, 0, mgl_fltk_tmp, 0);
pthread_detach(tmp); // run window handling in the separate thread
for(int i=0;i<10;i++) // do calculation
{
sleep(1); // which can be very long
pnt = mglPoint(2*mgl_rnd()-1,2*mgl_rnd()-1);
gr.Update(); // update window
}
return 0; // finish calculations and close the window
}
//-----------------------------------------------------------------------------
Most of the library was written by one person. This is a result of nearly a year of work (mostly in the evening and on holidays): I spent half a year to write the kernel and half a year to a year on extending, improving the library and writing documentation. This process continues now :). The autoconf/automake script was written mostly by D.Kulagin, and the export to IDTF was written mostly by M.Vidassov.
You can import data into a mglData instance and display it by Dens() function. For example, for black-and-white bitmap you can use the code: mglData bmp; bmp.Import("fname.png","wk"); gr->Dens(bmp,"wk");.
There are special classes (widgets) for these libraries: QMathGL for Qt, Fl_MathGL for FLTK and so on. If you don</samp>’t find the appropriate class then you can create your own widget that displays a bitmap using mglGraphAB::GetBits().
There are 2 steps: first you should create IDTF file, and later convert it to U3D. You can use U3D tools for converting IDTF file to U3D. It needs libharu 2.1.0 or later. For installation use ./bootstrap, ./configure, make, sudo make install. It provides IDTFConverter program for converting text files *.idtf to binary files *.u3d. The latter can be included into PDF.
First, you should download new font files from here or from here. Next, you should load the font files into mglGraph class instance gr by the following command: gr->SetFont(new mglFont(fontname,path));. Here fontname is the base font name like ‘STIX’ and path sets the location of font files. Use gr->SetFont(NULL); to start using the default font.
Just set a negative value for TickLen. For example, use gr->SetTickLen(-0.1);.
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
The MathGL library has interfaces for a set of languages. Most of them are based on the C interface via SWIG tool. There are Python, Java, Octave, Lisp, C#, Guile, Lua, Modula 3, Ocaml, Perl, PHP, Pike, R, Ruby, and Tcl interfaces. Also there is a Fortran interface which has a similar set of functions, but slightly different types of arguments (integers instead of pointers). These functions are marked as [C function]. Some of the languages listed above support classes (like Python). For them, a special wrapper was written. These classes and functions are marked as (Python). Finally, a special command language MGL was written for a faster access to C++ plotting functions. Corresponding scripts can be executed separately (by UDAV, mgl2png, mgl2eps and so on) or from the C++ code (see section mglParse class). These commands are described in MGL language.
| 1.6.1 C interface | ||
| 1.6.2 Python interface |
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
The C interface is a base for many other interfaces. It contains the pure C functions for most of the methods of MathGL classes. In distinction to C++ classes, C functions must have an argument HMGL (for graphics) and/or HMDT (for data arrays), which specifies the object for drawing or manipulating (changing). So, firstly, the user has to create this object by the function mgl_create_*() and has to delete it after the use by function mgl_delete_*().
All C functions are described in the header file #include <mgl/mgl_c.h> and use variables of the following types:
HMGL — Pointer to class mglGraph (see section MathGL core).
HMDT — Pointer to class mglData (see section mglData class).
HMPR — Pointer to class mglParse (see section mglParse class)..
These variables contain identifiers for graphics drawing objects and for the data objects.
Fortran functions/subroutines have the same names as C functions. However, there is a difference. Variable of type HMGL, HMDT must be an integer with sufficient size (integer*4 in the 32-bit operating system or integer*8 in the 64-bit operating system). All C functions are subroutines in Fortran, which are called by operator call. The exceptions are functions, which return variables of types HMGL or HMDT. These functions should be declared as integer in Fortran code. Also, one should keep in mind that strings in Fortran are denoted by </samp>’ symbol, not the " symbol.
Create and delete objects
HMGL mgl_create_graph_zb (int width, int height)Create the instance of class mglGraphZB with specified sizes.
HMGL mgl_create_graph_glut (int (*draw)(HMGL gr, void *p), const char *title, void *par)Create the instance of class mglGraphGLUT and the connected GLUT window. Only one GLUT window can be opened at once. Argument description can be found in mglGraphAB class.
HMGL mgl_create_graph_fltk (int (*draw)(HMGL gr, void *p), const char *title, void *par)Create the instance of class mglGraphFLTK and the connected FLTK window. Several windows can be opened at the same time. However user must call mgl_fltk_run() function to start the message handling cycle. Argument description can be found in mglGraphAB class. Note that draw can be NULL for displaying static bitmaps only (no animation or slides).
HMGL mgl_create_graph_qt (int (*draw)(HMGL gr, void *p), const char *title, void *par)Create the instance of class mglGraphQT and the connected Qt window. Several windows can be opened at the same time. However user must call mgl_qt_run() function to start the message handling cycle. Arguments description can be found in mglGraphAB class. Note, that draw can be NULL for displaying static bitmaps only (no animation or slides).
void mgl_fltk_run ()Start FLTK message handling cycle. A normal program will end main() function with return mgl_fltk_run();.
void mgl_fltk_thread ()Start FLTK message handling cycle. In distinction to mgl_fltk_run() the loop is started in a separate thread, so that program continues immediately.
void mgl_qt_run ()Start Qt message handling cycle. A normal program will end main() function with return mgl_qt_run();. Alternatively, the user may setup Qt application by direct Qt function calls.
void mgl_qt_thread ()Start Qt message handling cycle. In distinction to mgl_qt_run() the loop is started in separate thread so that the program continues immediately.
void mgl_set_show_mouse_pos (HMGL graph, int enable)Switch to show or not in the widget the last mouse click position.
void mgl_get_last_mouse_pos (HMGL graph, float *x, float *y, float *z)Last position of mouse click.
void mgl_calc_xyz (HMGL graph, int xs, int ys, float *x, float *y, float *z)Calculate 3D coordinate {x,y,z} for screen point {xs,ys}. At this moment, it ignores perspective and transformation formulas (curvilinear coordinates). The calculations are done for the last used InPlot (see section Transformation matrix).
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
MathGL provides the interface to a set of languages via SWIG library. Some of these languages support classes. The typical example is Python – which is named in this chapter</samp>’s title.
To use Python classes just execute ‘import mathgl’. The simplest example will be:
import mathgl a=mathgl.mglGraph() a.Box() a.WritePNG(</samp>’test.png</samp>’)
Alternatively you can import all classes from mathgl module and easily access MathGL classes like this:
from mathgl import * a=mglGraph() a.Box() a.WritePNG(</samp>’test.png</samp>’)
This becomes useful if you create many mglData objects, for example.
There are 2 classes in Python interface:
mglGraph
– provide practically the same functionality as C++ class mglGraph (see section MathGL core). But it is not an abstract class and it allows one to select at construction stage which plotter (ZB or PS and so on) will be used.
mglData
– is exactly the same class as C++ mglData (see section mglData class), but an additional feature to access data values is added. You can use a construct like this: dat[i]=sth; or sth=dat[i] where flat representation of data is used (i.e., i can be in range 0...nx*nx*nz-1). You can also import NumPy arrays as input arguments: mgl_dat = mglData(numpy_dat);.
To use Python classes just execute ‘import mathgl’. The simplest example will be:
import mathgl a=mathgl.mglGraph() a.Box() a.WritePNG(</samp>’test.png</samp>’)
Alternatively, you can import all the classes from mathgl module and easily access MathGL classes:
from mathgl import * a=mglGraph() a.Box() a.WritePNG(</samp>’test.png</samp>’)
This is useful if you create many mglData objects, for example.
There are 2 classes in Python interface:
mglGraph
– provide practically the same functionality as C++ class mglGraph (see section MathGL core). But it is not an abstract class and it allows one to select at the construction stage which plotter (ZB or PS and so on) will be used.
mglData
– is exactly the same class as C++ mglData (see section mglData class), but an additional feature to access data values is added. You can use a construct like this: dat[i]=sth; or sth=dat[i] where flat representation of data is used (i.e., i can be in range 0...nx*nx*nz-1).
There is one main difference from C++ classes – Python class mglGraph does not have variables (options). All the corresponding features are moved to methods.
The core of MathGL Python class is the mglGraph class. It contains a lot of plotting functions for 1D, 2D and 3D plots. So most of the sections describe its methods. Its constructor has the following arguments:
int kind=0, int width=600, int height=400)Create the instance of class mglGraph with specified sizes width and height. Parameter type may have following values: ‘0’ – use mglGraphZB plotter (default), ‘1’ – use mglGraphPS plotter, ‘2’ – use mglGraphGL plotter, ‘3’ – use mglGraphIDTF plotter.
There is one difference from C++ classes – Python class mglGraph does not have variables (options). All the corresponding features are moved to methods.
The core of MathGL Python class is the mglGraph class. It contains a lot of plotting functions for 1D, 2D and 3D plots. So most of the sections describe its methods. Its constructor has the following arguments:
int kind=0, int width=600, int height=400)Create the instance of class mglGraph with specified sizes width and height. Parameter type may have following values: ‘0’ – use mglGraphZB plotter (default), ‘1’ – use mglGraphPS plotter, ‘2’ – use mglGraphGL plotter, ‘3’ – use mglGraphIDTF plotter.
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
| [ << ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
This document was generated by Alexey Balakin on May 2, 2013 using texi2html 1.82.