| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
This chapter contain information about basic and advanced MathGL, hints and samples for all types of graphics. I recommend you read first 2 sections one after another and at least look on “Hints” section. Also I recommend you to look at General concepts and FAQ. Sample code for some of these examples can be found in http://mathgl.sf.net/pictures.html and in Samples.
| 2.1 Basic usage | ||
| 2.2 Advanced usage | ||
| 2.3 Data handling | ||
| 2.4 Data plotting | ||
| 2.5 C/Fortran interface | ||
| 2.6 MathGL and PyQt | ||
| 2.7 Hints |
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
MathGL library can be used by several manners. Each has positive and negative sides:
Positive side is the possibility to view the plot at once and to modify it (rotate, zoom or switch on transparency or lighting) by hand or by mouse. Negative sides are: the need of X-terminal and limitation consisting in working with the only one set of data at a time.
Positive aspects are: batch processing of similar data set (for example, a set of resulting data files for different calculation parameters), running from the console program (including the cluster calculation), fast and automated drawing, saving pictures for further analysis (or demonstration). Negative sides are: the usage of the external program for picture viewing. Also, the data plotting is non-visual. So, you have to imagine the picture (view angles, lighting and so on) before the plotting. I recommend to use graphical window for determining the optimal parameters of plotting on the base of some typical data set. And later use these parameters for batch processing in console program.
In this case the programmer has more freedom in selecting the window libraries (not only FLTK or GLUT), in positioning and surroundings control and so on. I recommend to use such way for “settled” programs.
Let me consider the aforesaid in more detail.
| 2.1.1 Using FLTK/Qt/GLUT window | ||
| 2.1.2 Drawing to file | ||
| 2.1.3 Drawing in memory | ||
| 2.1.4 Using QMathGL |
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
The “interactive” way of drawing in MathGL consists in window creation with help of class mglGraphFLTK, mglGraphQT or mglGraphGLUT (see section Widget classes) and the following drawing in this window. There is a corresponding code:
int sample(mglGraph *gr, void *)
{
gr->Rotate(60,40);
gr->Box();
return 0;
}
//-----------------------------------------------------
int main(int argc,char **argv)
{
mglGraphFLTK gr;
gr.Window(argc,argv,sample,"MathGL examples");
return mglFlRun();
}
Here function sample is defined. This function does all drawing. Other function main is entry point function for console program. Arguments of main should be transfered to Window() since it may contain OS specific information (see section mglGraphAB class).
Alternatively you can create yours own class inherited from class mglDraw and re-implement the function Draw() in it:
class Foo : public mglDraw
{
public:
int Draw(mglGraph *gr);
} foo;
//-----------------------------------------------------
int Foo::Draw(mglGraph *gr)
{
gr->Rotate(60,40);
gr->Box();
return 0;
}
//-----------------------------------------------------
int main(int argc,char **argv)
{
mglGraphFLTK gr;
gr.Window(argc,argv,"MathGL examples",&foo);
return mglFlRun();
}
The similar code can be written for mglGraphQT or for mglGraphGLUT window (function sample() is the same):
int main(int argc,char **argv)
{
mglGraphGLUT gr;
gr.Window(argc,argv,sample,"MathGL examples");
return 0;
}
The rotation, shift, zooming, switching on/off transparency and lighting can be done with help of tool-buttons (for mglGraphFLTK and mglGraphQT) or by hot-keys: ‘a’, ‘d’, ‘w’, ‘s’ for plot rotation, ‘r’ and ‘f’ switching on/off transparency and lighting. Press ‘x’ for exit (or closing the window).
In this example function sample rotates axes (Rotate(), see section Transformation matrix) and draws the bounding box (Box()). Drawing procedure is separated in a function since it will be used on demand when window canvas needs to be redrawn. Widget classes (mglGraphFLTK, mglGraphGLUT and so on) support a delayed drawing, when all plotting functions are called once at the beginning of writing to memory lists. Further program displays the saved lists faster. Resulting redrawing will be faster but it requires sufficient memory. Several lists (frames) can be displayed one after another (by pressing ‘,’, ‘.’) or run as cinema. To switch these feature on one needs to modify function sample:
int sample1(mglGraph *gr, void *)
{
gr->NewFrame(); // the first frame
gr->Rotate(60,40);
gr->Box();
gr->EndFrame(); // end of the first frame
gr->NewFrame(); // the second frame
gr->Box();
gr->Axis("xy");
gr->EndFrame(); // end of the second frame
return GetNumFrame(); // returns the frame number
}
First, the function creates a frame NewFrame() for rotated axes and draws the bounding box. After the frame drawing the function EndFrame() must be called! The second frame contains the bounding box and axes Axis("xy") in the initial (unrotated) coordinates. Function sample returns the number of created frames GetNumFrame().
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
Another way of using MathGL library is the direct picture writing to file. It is most usable for plot creating during calculation or for using of small programs (like Matlab or Scilab scripts) for visualizing repetitive sets of data. But the speed of drawing is much higher in comparison with a script language. There are two classes for exporting in file: class mglGraphZB saves in bitmap format (like PNG), mglGraphPS saves in vector PostScript format (see section Plotter classes).
The following code produces a bitmap PNG picture:
int main(int ,char **)
{
mglGraphZB gr;
gr.Alpha(true);
gr.Light(true); gr.Light(0,mglPoint(1,0,-1));
sample(&gr,NULL); // The same drawing function.
gr.WritePNG("test.png"); // Don't forget to save the result!
return 0;
}
The only difference from the previous (using windows) variant is manual switching the transparency Alpha and lightning Light on, if the plot requires it. The using of frames is not advisable since the whole image is prepared each time. If function sample contains frames then each frame will be saved to a separate file. In principle, one does not need to separate drawing functions in case of direct file writing in consequence of the single calling of this function for each picture. However, one may use the same drawing procedure to create a plot with changed parameters, to export in different file types, to emphasize the drawing code and so on. So, in future I will put the drawing in separate function.
The code for export in vector EPS file looks the same:
int main(int ,char **)
{
mglGraphPS gr;
gr.Light(true); gr.Light(0,mglPoint(1,0,-1));
sample(&gr,NULL); // The same drawing function.
gr.WriteEPS("test.eps"); // Don't forget to save the result!
return 0;
}
The differences from the using of bitmap picture are: applying of the other class mglGraphPS, and writing to other format (function WriteEPS() instead of function WritePNG()). Moreover, there is no switching of the plot transparency Alpha since EPS format does not support it. Possibly I shall include transparency in future by program emulation.
Classes mglGraphZB and mglGraphPS have some merits and demerits. Class mglGraphZB draws beautiful surface with transparency, smoothed colors and lightning, but the output picture is bitmap, that leads to a bad scalability. On the contrary, class mglGraphPS creates vector file with excellent scalability. But file has large size (especially for surfaces), it does not support transparency and color smoothing. So, vector picture looks stylish but a bit angularly.
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
The last way of MathGL using is the drawing in memory. Class mglGraphZB allows one to create a bitmap picture in memory. Further this picture can be displayed in window by some window libraries (like wxWidgets, FLTK, Windows GDI and so on). For example, the code for drawing in wxWidget library looks like:
void MyForm::OnPaint(wxPaintEvent& event)
{
int w,h,x,y;
GetClientSize(&w,&h); // size of the picture
mglGraphZB gr(w,h);
gr.Alpha(true); // draws something using MathGL
gr.Light(true); gr.Light(0,mglPoint(1,0,-1));
sample(&gr,NULL);
wxImage img(w,h,gr.GetBits(),true);
ToolBar->GetSize(&x,&y); // gets a height of the toolbar if any
wxPaintDC dc(this); // and draws it
dc.DrawBitmap(wxBitmap(img),0,y);
}
The drawing in other libraries is most the same.
For example, FLTK code will look like
void Fl_MyWidget::draw()
{
mglGraphZB gr(w(),h());
gr.Alpha(true); // draws something using MathGL
gr.Light(true); gr.Light(0,mglPoint(1,0,-1));
sample(&gr,NULL);
fl_draw_image(gr.GetBits(), x(), y(), gr.GetWidth(), gr.GetHeight(), 3);
}
Qt code will look like
void MyWidget::paintEvent(QPaintEvent *)
{
mglGraphZB gr(w(),h());
gr.Alpha(true); // draws something using MathGL
gr.Light(true); gr.Light(0,mglPoint(1,0,-1));
sample(&gr,NULL);
// Qt don't support RGB format as is. So, let convert it to BGRN.
const uchar *bb = gr.GetBits();
register long i, w=gr.GetWidth(), h=gr.GetHeight();
*buf = new uchar[4*w*h];
for(i=0;i<w*h;i++)
{
(*buf)[4*i] = bb[3*i+2];
(*buf)[4*i+1] = bb[3*i+1];
(*buf)[4*i+2] = bb[3*i];
(*buf)[4*i+3] = 255;
}
QPixmap pic = QPixmap::fromImage(QImage(*buf, w, h, QImage::Format_RGB32));
QPainter paint;
paint.begin(this); paint.drawPixmap(0,0,pic); paint.end();
delete []buf;
}
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
MathGL have several interface widgets for different widget libraries. There are QMathGL for Qt, Fl_MathGL for FLTK in MathGL v.1.8. These classes provide control which display MathGL graphics. Unfortunately there is no uniform interface for widget classes because all libraries have slightly different set of functions, features and so on. However the usage of MathGL widgets is rather simple. Let me show it on the example of QMathGL.
First of all you have to define the drawing function or inherit a class from mglDraw class. After it just create a window and setup QMathGL instance as any other Qt widget:
int main(int argc,char **argv)
{
QApplication a(argc,argv);
QMainWindow *Wnd = new QMainWindow;
Wnd->resize(650,480); // for fill up the QMGL, menu and toolbars
Wnd->setWindowTitle(title);
// here I allow to scroll QMathGL -- the case
// then user want to prepare huge picture
QScrollArea *scroll = new QScrollArea(Wnd);
// Create and setup QMathGL
QMathGL *QMGL = new QMathGL(Wnd);
QMGL->setPopup(popup); // if you want to setup popup menu for QMGL
QMGL->setDraw(sample, NULL);
// or use QMGL->setDraw(foo); for instance of class Foo:public mglDraw
QMGL->update();
// continue other setup (menu, toolbar and so on)
makeMenu();
scroll->setWidget(QMGL);
Wnd->setCentralWidget(scroll);
Wnd->show();
return a.exec();
}
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
Now I show several non-obvious features of MathGL: several subplots in a single picture, curvilinear coordinates, text printing and so on. Generally you may miss this section at first reading, but I don’t recommend it.
| 2.2.1 Subplots | ||
| 2.2.2 Axis and grids | ||
| 2.2.3 Curvilinear coordinates | ||
| 2.2.4 Text printing example | ||
| 2.2.5 Animation |
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
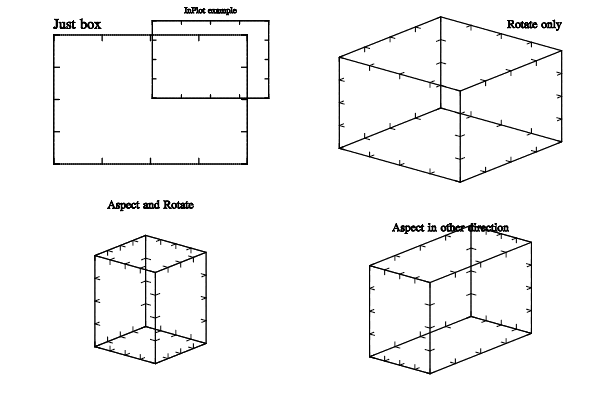
Let me demonstrate possibilities of axes transformation. MathGL has the following functions: SubPlot, InPlot, Aspect and Rotate (see section Transformation matrix). The order of their calling is strictly determined. First, one changes the position of axes in image area (functions SubPlot and InPlot). After that one may rotate the plot (function Rotate). Finally, one may change aspects of axes (function Aspect). The following code illustrates the aforesaid it:
int sample(mglGraph *gr, void *)
{
gr->SubPlot(2,2,0);
gr->Box();
gr->Puts(mglPoint(-1,1.1,1),"Just box","rL");
gr->InPlot(0.2,0.5,0.7,1);
gr->Box();
gr->Puts(mglPoint(0,1.2,1),"InPlot example");
gr->SubPlot(2,2,1);
gr->Rotate(60,40);
gr->Aspect(1,1,1);
gr->Box();
gr->Puts(mglPoint(1,1,1.5),"Rotate only","rR");
gr->SubPlot(2,2,2);
gr->Rotate(60,40);
gr->Aspect(1,1,2);
gr->Box();
gr->Puts(mglPoint(0,0,2),"Aspect and Rotate");
gr->SubPlot(2,2,3);
gr->Rotate(60,40);
gr->Aspect(1,2,2);
gr->Box();
gr->Puts(mglPoint(0,0,1.5),"Aspect in other direction");
return 0;
}
Here I used function Puts for printing the text in arbitrary position of picture (see section Text printing). Text coordinates and size are connected with axes. However, text coordinates may be everywhere, including the outside the bounding box. I shall show its features later in See section Text printing example.

Example of several subplots on the single picture.
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
MathGL library can draw not only the bounding box but also the axes, grids, labels and so on. The limits of axes and their origin (the point of intersection) are determined by function Axis(). Also you can use XRange(), YRange(), ZRange() functions (see section Ranges (bounding box)). Ticks on axis are specified by function SetTicks (see section Ticks). First argument the direction for each change will be applied. Second argument gives the step between ticks (if positive) or gives the number of ticks on the axis (if negative) or set to use logarithmic ticks (if zero). Third argument gives numbers of sub-ticks between ticks (default is zero). Last argument define the initial ticks position.
Function Axis draws axes. Its textual string shows in which directions the axis or axes will be drawn (by default "xyz", function draws axes in all directions). Function Grid draws grid perpendicularly to specified directions. Example of axes and grid drawing is:
int sample(mglGraph *gr, void *)
{
gr->SubPlot(2,2,0);
gr->SetTicks('x', 0.4, 3); // sets tick step to 0.5
gr->SetTicks('y', 0.4, 3); // and draws 3 subticks
gr->Box(); // should be after the ticks change
gr->Axis("xy");
gr->Grid();
gr->Puts(mglPoint(0,1.3,1),"Axis and grid");
gr->SetTicks('x'); gr->SetTicks('y'); // restore back
gr->Axis(mglPoint(-1,-1,-1),mglPoint(1,1,1),mglPoint(0,0,0));
gr->SubPlot(2,2,1);
gr->Rotate(60,40);
gr->Axis();
gr->Label('x',"x");
gr->Label('y',"y");
gr->Label('z',"z");
gr->Puts(mglPoint(0,0,1.5),"Axis and labels");
gr->SubPlot(2,2,2);
gr->Rotate(60,40);
gr->SetTicks('x', 0.2); gr->SetTicks('y', 0.2);
gr->SetTicks('z', 0.2); // too low step of ticks
gr->Axis(mglPoint(-1,-1,-1),mglPoint(1,1,1),mglPoint(-1,-1,-1));
gr->Axis();
gr->Grid();
gr->Puts(mglPoint(0,0,1.5),"Shift origin and add grid");
gr->Puts(mglPoint(0,0,1.2),"(note, too many ticks)");
gr->SubPlot(2,2,3);
gr->Rotate(60,40);
gr->SetTicks('x', -6); // decrease the number of ticks
gr->SetTicks('y', -6);
gr->Axis("yz");
gr->Label('y',"Y axis",0);
gr->Label('z',"Z axis",0);
gr->Puts(mglPoint(0,0,1.5),"Remove X axis, and");
gr->Puts(mglPoint(0,0,1.2),"decrease number of ticks");
return 0;
}
This example shows the importance of the correct choosing of the number of ticks on axis. If tick step is too small then its text may overlap and becomes unreadable. This code has the example of Label function. It draws label for axis in specified direction. The text position on axis is specified by third argument of Label function. If it is positive then then text is drawn near the axis maximum, if negative then the same takes place near the minimum of axis, if zero - then at the center of axis.
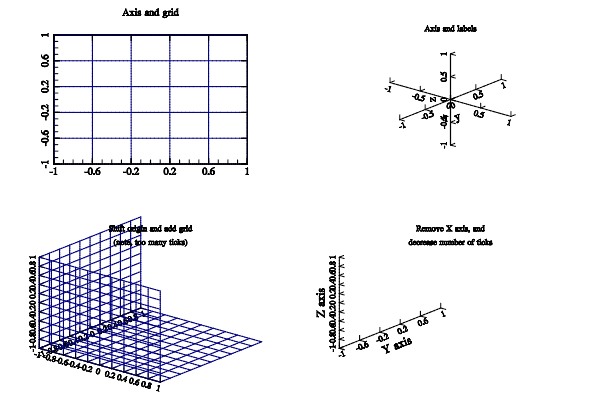
Example of setting up axis range and axis ticks.
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
Now let use curvilinear coordinates. In difference from other systems of plot creation, MathGL uses textual formulas for connection of the old (data) and new (output) coordinates. This allows one to plot in arbitrary coordinates. The following code plots the line y=0, z=0 in Cartesian, polar, parabolic and spiral coordinates:
int sample(mglGraph *gr, void *)
{
mglData x(50),y(50),z(50);
y.Fill(0.5,0.5);
x.Fill(-1,1); // creates data arrays
gr->Axis(mglPoint(-1,-1,-1),mglPoint(1,1,1),mglPoint(-1,1,-1));
gr->dz = 0.5; // sets tick step to 0.5
gr->SubPlot(2,2,0);
gr->Rotate(60,40);
gr->Plot(x,y,z,"r2");
gr->Axis(); gr->Grid();
gr->Puts(mglPoint(0,1.3,1),"Cartesian");
gr->SubPlot(2,2,1);
gr->SetFunc("y*sin(pi*x)","y*cos(pi*x)",0);
gr->Rotate(60,40);
gr->Plot(x,y,z,"r2");
gr->Axis(); gr->Grid();
gr->Puts(mglPoint(0,1.3,1),"Cylindrical");
gr->SubPlot(2,2,2);
gr->Rotate(60,40);
gr->SetFunc("2*y*x","y*y - x*x",0);
gr->Plot(x,y,z,"r2");
gr->Axis(); gr->Grid();
gr->Puts(mglPoint(0,1.3,1),"Parabolic");
gr->SubPlot(2,2,3);
gr->Rotate(60,40);
gr->SetFunc("y*sin(pi*x)","y*cos(pi*x)","x+z");
gr->Plot(x,y,z,"r2");
gr->Axis(); gr->Grid();
gr->Puts(mglPoint(0,1.3,1),"Spiral");
return 0;
}
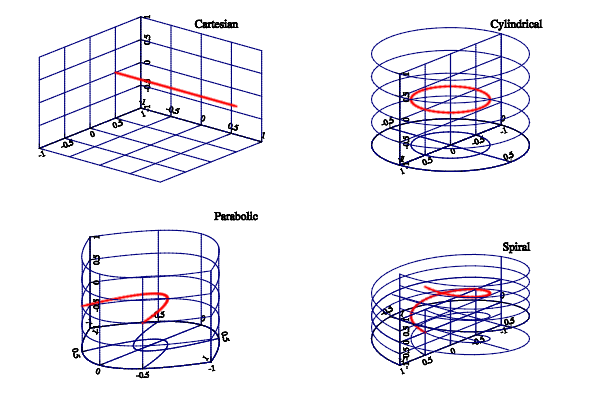
Example of curvilinear coordinates
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
MathGL prints text by vector font. There are functions for manual specifying of text position (like Puts) and for its automatic selection (like Label, Legend and so on). MathGL prints text always in specified position even if it lies outside the bounding box. The default size of font is specified by variables FontSize (see section Font settings). However, the actual size of output string depends on position of axes (depends on functions SubPlot, InPlot). The switching of the font style (italic, bold, wire and so on) can be done for the whole string (by function parameter) or inside the string. By default MathGL parses TeX-like commands for symbols and indexes (see see section Font styles). Example of MathGL font drawing is:
int sample(mglGraph *gr, void *)
{
setlocale(LC_CTYPE, "ru_RU.cp1251");
gr->Puts(mglPoint(0,1),"Text can be in ASCII and in Unicode");
gr->Puts(mglPoint(0,0.6),"It can be \\wire{wire}, \\big{big} "
"or #r{colored}");
gr->Puts(mglPoint(0,0.2),"One can change style in string: "
"\\b{bold}, \\i{italic, \\b{both}}");
gr->Puts(mglPoint(0,-0.2),"Easy to \\a{overline} or "
"\\u{underline}");
gr->Puts(mglPoint(0,-0.6),"Easy to change indexes "
"^{up} _{down} @{center}");
gr->Puts(mglPoint(0,-1),"It parse TeX: \\int \\alpha \\cdot "
"\\sqrt3{sin(\\pi x)^2 + \\gamma_{i_k}} dx");
return 0;
}

Example of text printing with different font effects
Another example demonstrate the features of TeX formula parsing.
int sample(mglGraph *gr, void *)
{
gr->Puts(mglPoint(0), "\\sqrt{\\frac{\\alpha^{\\gamma^2}+"
"\\overset 1{\\big\\infty}}{\\sqrt3{2+b}}}", 0, -4);
return 0;
}
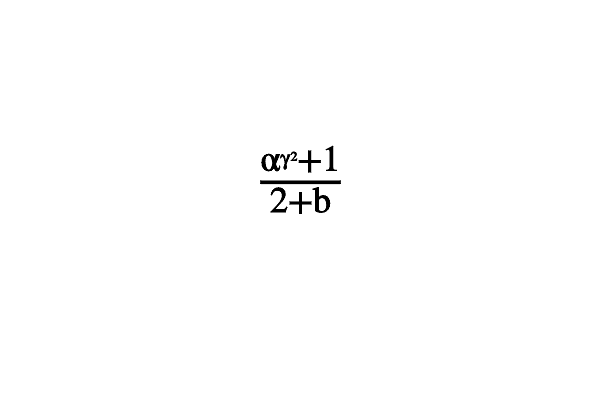
Example of TeX formula parsing
Finally you can change font during execution (this work well for mglGraphZB class only).
int sample(mglGraph *gr, void *)
{
float h=1.1, d=0.25;
gr->LoadFont("STIX"); gr->Puts(mglPoint(0,h), "default font (STIX)");
gr->LoadFont("adventor"); gr->Puts(mglPoint(0,h-d), "adventor font");
gr->LoadFont("bonum"); gr->Puts(mglPoint(0,h-2*d), "bonum font");
gr->LoadFont("chorus"); gr->Puts(mglPoint(0,h-3*d), "chorus font");
gr->LoadFont("cursor"); gr->Puts(mglPoint(0,h-4*d), "cursor font");
gr->LoadFont("heros"); gr->Puts(mglPoint(0,h-5*d), "heros font");
gr->LoadFont("heroscn"); gr->Puts(mglPoint(0,h-6*d), "heroscn font");
gr->LoadFont("pagella"); gr->Puts(mglPoint(0,h-7*d), "pagella font");
gr->LoadFont("schola"); gr->Puts(mglPoint(0,h-8*d), "schola font");
gr->LoadFont("termes"); gr->Puts(mglPoint(0,h-9*d), "termes font");
}

Example of font face changing.
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
You can make animation by several methods in MathGL: by export in animated GIF, or by save each frame in separate file (usually JPEG) and convert these files into movie. Let me show both methods.
The simplest methods is making animated GIF. There are 3 steps: (1) open GIF file by StartGIF() function; (2) create the frames by calling NewFrame() before and EndFrame() after plotting; (3) close GIF by CloseGIF() function. So the simplest code for “running” sinusoid will look like this:
int sample(mglGraph *gr, void *)
{
mglData dat(100);
char str[32];
gr->StartGIF("sample.gif");
for(int i=0;i<100;i++)
{
gr->NewFrame(); // start frame
gr->Box(); // some plotting
sprintf(str,"sin(pi*x+%g*pi)",0.02*i);
dat.Modify(str);
gr->Plot(dat,"b");
gr->EndFrame(); // end frame
}
gr->CloseGIF();
return 0;
}
The second way is saving each frame in separate file (usually JPEG) and later make the movie from them. MathGL have special function for saving frames – it is WriteFrame(). This function save each frame with automatic name ‘frame0001.jpg, frame0002.jpg’ and so on. Here prefix ‘frame’ is defined by PlotId variable of mglGraph class. So the similar code will look like this:
int sample(mglGraph *gr, void *)
{
mglData dat(100);
char str[32];
for(int i=0;i<100;i++)
{
gr->NewFrame(); // start frame
gr->Box(); // some plotting
sprintf(str,"sin(pi*x+%g*pi)",0.02*i);
dat.Modify(str);
gr->Plot(dat,"b");
gr->EndFrame(); // end frame
gr->WriteFrame(); // save frame
}
return 0;
}
Created files can be converted to movie by help of a lot of programs. For example, you can use ImageMagic (command ‘convert frame*.jpg movie.mpg’), MPEG library, GIMP and so on.
Finally, you can use mgl2gif tool for doing the same with MGL scripts (see section Utilities for parsing MGL).
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
Class mglData contains all functions for the data handling in MathGL (see section mglData class). There are several matters why I use class mglData but not a single array: it does not depend on type of data (float or double), sizes of data arrays are kept with data, memory working is simpler and safer.
| 2.3.1 Array creation | ||
| 2.3.2 Data changing |
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
One can put the data in mglData instance by several ways. Let us do it for sinus function:
mglData variable
double *a = new double[50];
for(int i=0;i<50;i++) a[i] = sin(M_PI*i/49.);
mglData y;
y.Set(a,50);
mglData instance of the desired size and then to work directly with data in this variable
mglData y(50);
for(int i=0;i<50;i++) y.a[i] = sin(M_PI*i/49.);
mglData instance by textual formula with the help of Modify() function
mglData y(50);
y.Modify("sin(pi*x)");
mglData y(50);
y.Fill(0,M_PI);
y.Modify("sin(u)");
FILE *fp=fopen("sin.dat","wt"); // create file first
for(int i=0;i<50;i++) fprintf(fp,"%g\n",sin(M_PI*i/49.));
fclose(fp);
mglData y("sin.dat"); // load it
FILE *fp-fopen("sin.dat","wt"); // create large file first
for(int i=0;i<70;i++) fprintf(fp,"%g\n",sin(M_PI*i/49.));
fclose(fp);
mglData y;
y.Read("sin.dat",50); // load it
Creation of 2d- and 3d-arrays is mostly the same. But one should keep in mind that class mglData uses flat data representation. For example, matrix 30*40 is presented as flat (1d-) array with length 30*40=1200 (nx=30, ny=40). The element with indexes {i,j} is a[i+nx*j]. So for 2d array we have:
mglData z(30,40);
for(int i=0;i<30;i++) for(int j=0;j<40;j++)
z.a[i+30*j] = sin(M_PI*i/29.)*sin(M_PI*j/39.);
or by using Modify() function
mglData z(30,40);
z.Modify("sin(pi*x)*cos(pi*y)");
The only non-obvious thing here is using multidimensional arrays in C/C++, i.e. arrays defined like float dat[40][30];. Since, formaly this arrays element dat[i] can address the memory in arbitrary place you should use the proper function to convert such arrays to mglData object. For C++ this is functions like mglData::Set(float **dat, int N1, int N2);. For C this is functions like mgl_data_set_float2(HMDT d, const float **dat, int N1, int N2);. At this, you should keep in mind that nx=N2 and ny=N1 after conversion.
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
MathGL has functions for data processing: differentiating, integrating, smoothing and so on (for more detail, see section mglData class). Let us consider some examples. The simplest ones are integration and differentiation. The direction in which operation will be performed is specified by textual string, which may contain symbols ‘x’, ‘y’ or ‘z’. For example, the call of Diff("x") will differentiate data along ‘x’ direction; the call of Integral("xy") perform the double integration of data along ‘x’ and ‘y’ directions; the call of Diff2("xyz") will apply 3d Laplace operator to data and so on. Example of this operations on 2d array a=x*y is presented in code:
int sample(mglGraph *gr, void *)
{
mglData a(30,40); a.Modify("x*y");
gr->Axis(mglPoint(0,0,0),mglPoint(1,1,1));
gr->SubPlot(2,2,0); gr->Rotate(60,40);
gr->Surf(a); gr->Box();
gr->Puts(mglPoint(0.7,1,1.2),"a(x,y)");
gr->SubPlot(2,2,1); gr->Rotate(60,40);
a.Diff("x"); gr->Surf(a); gr->Box();
gr->Puts(mglPoint(0.7,1,1.2),"da/dx");
gr->SubPlot(2,2,2); gr->Rotate(60,40);
a.Integral("xy"); gr->Surf(a); gr->Box();
gr->Puts(mglPoint(0.7,1,1.2),"\\int da/dx dxdy");
gr->SubPlot(2,2,3); gr->Rotate(60,40);
a.Diff2("y"); gr->Surf(a); gr->Box();
gr->Puts(mglPoint(0.7,1,1.2),"\\int {d^2}a/dxdy dx");
return 0;
}
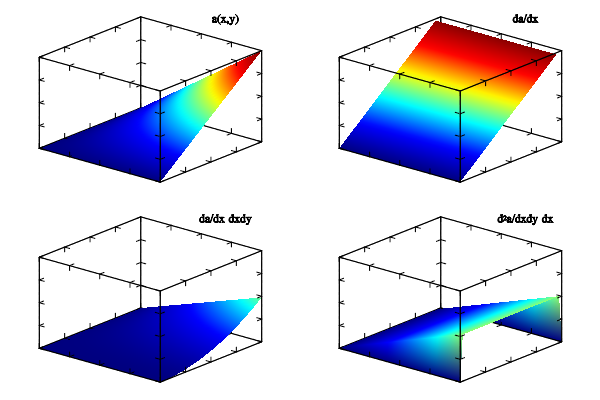
Example of data differentiation and integration
Data smoothing (function Smooth()) is more interesting and important. This function has 2 main arguments: type of smoothing and its direction. Now 4 methods are supported: SMOOTH_NONE does nothing for delta=0 or approaches data to zero with the step delta, SMOOTH_LINE_3 linear averaging by 3 points, SMOOTH_LINE_5 linear averaging by 5 points, SMOOTH_QUAD_5 quadratic averaging by 5 points. Let me demonstrate it for 1d case:
int sample(mglGraph *gr, void *)
{
mglData y0(30),y1,y2,y3;
y0.Modify("0.4*sin(2*pi*x)+0.3*cos(3*pi*x)-0.4*sin(4*pi*x)+0.2*rnd");
y1=y0; y1.Smooth(SMOOTH_LINE_3);
y2=y0; y2.Smooth(SMOOTH_LINE_5);
y3=y0; y3.Smooth(SMOOTH_QUAD_5);
gr->Plot(y0,"k"); gr->AddLegend("NONE","k");
gr->Plot(y1,"r"); gr->AddLegend("LINE_3","r");
gr->Plot(y2,"g"); gr->AddLegend("LINE_5","g");
gr->Plot(y3,"b"); gr->AddLegend("QUAD_5","b");
gr->Legend(); gr->Box();
return 0;
}
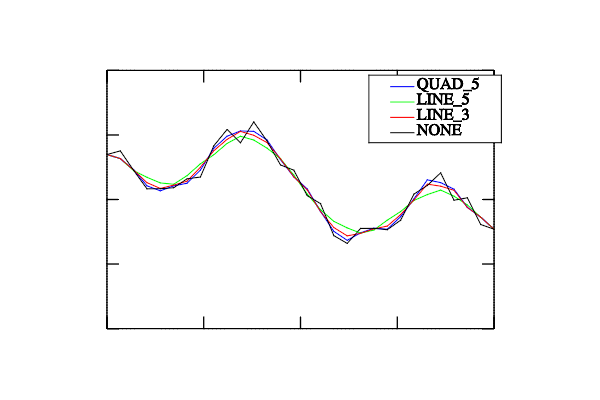
Example of data smoothing
Finally one can create new data arrays on base of the existing one: extract slice, row or column of data (SubData()), summarize along some of direction(s) (Sum()), find distribution of data elements (Hist()). Note, that all these functions are not thread-safe because they use static internal variable for output array. In particular, the using of several of them in arguments of the same function will lead to unpredictable result.
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
Let me now show how to plot the data. MathGL generally has 2 types of plotting functions. Simple variant requires a single data array for plotting, other data (coordinates) are considered uniformly distributed in interval Min*Max. Second variant requires data arrays for all coordinates. It allows one to plot rather complex multivalent curves and surfaces (in case of parametric dependencies). Argument setting to default values allows one to plot data in standard form. Manual arguments setting gives possibility for fine tuning of colors, positions and view of graphics. Note, that the call of drawing function adds something to picture but does not clear the previous plots (as it does in Matlab). Another difference from Matlab is that all setup (like transparency, lightning, axis borders and so on) must be specified before plotting functions.
| 2.4.1 Plots for 1D data | ||
| 2.4.2 Plots for 2D data | ||
| 2.4.3 Plots for 3D data | ||
| 2.4.4 Surface transparency |
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
Term “1D data” means that data depend on single index (parameter) like curve in parametric form {x(i),y(i),z(i)}, i=1...n. There are 5 generally different types of data representations: simple line plot, line plot with filling under it, stairs plot, bar plot and vertical lines (see section 1D plotting). Each type of plotting has similar interface. There are 3D version and two 2D versions. One of last requires single array. The parameters of line and marks (see section Line styles) are specified by the string argument. If the string parameter is NULL then solid line with color from palette is used (see section Pallete and colors).
Below I shall show the features of 1D plotting on base of Plot() function (see section Plot). Let us start from sinus plot:
int sample(mglGraph *gr, void *)
{
mglData y0(50); y0.Modify("sin(pi*(2*x-1))");
gr->SubPlot(2,2,0);
gr->Plot(y0); gr->Box();
Style of line is not specified in Plot() function. So MathGL uses the solid line with first color of palette (this is blue). Next subplot shows array y1 with 2 rows:
gr->SubPlot(2,2,1);
mglData y1(50,2);
y1.Modify("sin(pi*2*x-pi)");
y1.Modify("cos(pi*2*x-pi)/2",1);
gr->Plot(y1); gr->Box();
As previously I did not specify the style of lines. As a result, MathGL again uses solid line with next colors in palette (there are green and red). Now let us plot a circle on the same subplot. The circle is parametric curve x=cos(\pi t), y=sin(\pi t). I will set the color of the circle (dark yellow, ‘Y’) and put marks ‘+’ at point position:
mglData x(50); x.Modify("cos(pi*2*x-pi)");
gr->Plot(x,y0,"Y+");
Note that solid line is used because I did not specify the type of line. The same picture can be achieved by Plot() and SubData()) functions. Let us draw ellipse by orange dash line:
gr->Plot(y1.SubData(-1,0),y1.SubData(-1,1),"q|");
Drawing in 3D space is mostly the same. Let us draw spiral with default line style. Now its color is 4-th color from palette (this is cyan):
gr->SubPlot(2,2,2); gr->Rotate(60,40);
mglData z(50); z.Modify("2*x-1");
gr->Plot(x,y0,z); gr->Box();
Functions Plot() and SubData()) make 3D curve plot but for single array. Use it to put circle marks on the previous plot:
mglData y2(10,3); y2.Modify("cos(pi*(2*x-1+y))");
y2.Modify("2*x-1",2);
gr->Plot(y2.SubData(-1,0),y2.SubData(-1,1),y2.SubData(-1,2),"bo ");
Note that line style is empty ‘ ’ here. Usage of other 1D plotting functions looks similar:
gr->SubPlot(2,2,3); gr->Rotate(60,40);
gr->Bars(x,y0,z,"r"); gr->Box();
return 0;
}
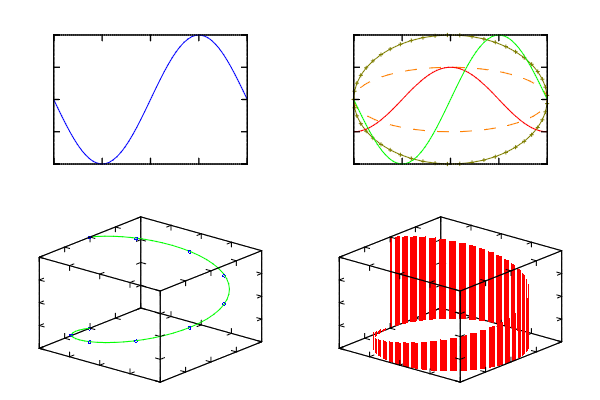
Example of 1D data plot
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
Surfaces Surf() and other 2D plots (see section 2D plotting) are drown the same simpler as 1D one. The difference is that the string parameter specifies not by line style but by the color scheme of the plot (see section Color scheme). Here I draw attention on 4 most interesting color schemes. There is gray scheme where color is changed from black to white (string ‘kw’) or from white to black (string ‘wk’). Another scheme is useful for accentuation of negative (by blue color) and positive (by red color) regions on plot (string ‘"BbwrR"’). Last one is the popular “jet” scheme (string ‘"BbcyrR"’).
Now I shall show the example of a surface drawing. At first let us switch lightning on
int sample(mglGraph *gr, void *)
{
gr->Light(true); gr->Light(0,mglPoint(0,0,1));
and draw the surface, considering coordinates x,y to be uniformly distributed in interval Min*Max
mglData a0(50,40);
a0.Modify("0.6*sin(2*pi*x)*sin(3*pi*y)+0.4*cos(3*pi*(x*y))");
gr->SubPlot(2,2,0); gr->Rotate(60,40);
gr->Surf(a0); gr->Box();
Color scheme was not specified. So previous color scheme is used. In this case it is default color scheme (“jet”) for the first plot. Next example is a sphere. The sphere is parametrically specified surface:
mglData x(50,40),y(50,40),z(50,40);
x.Modify("0.8*sin(2*pi*x)*sin(pi*y)");
y.Modify("0.8*cos(2*pi*x)*sin(pi*y)");
z.Modify("0.8*cos(pi*y)");
gr->SubPlot(2,2,1); gr->Rotate(60,40);
gr->Surf(x,y,z,"BbwrR");gr->Box();
I set color scheme to "BbwrR" that corresponds to red top and blue bottom of the sphere.
Surfaces will be plotted for each of slice of the data if nz>1. Next example draws surfaces for data arrays with nz=3:
mglData a1(50,40,3);
a1.Modify("0.6*sin(2*pi*x)*sin(3*pi*y)+0.4*cos(3*pi*(x*y))");
a1.Modify("0.6*cos(2*pi*x)*cos(3*pi*y)+0.4*sin(3*pi*(x*y))",1);
a1.Modify("0.6*cos(2*pi*x)*cos(3*pi*y)+0.4*cos(3*pi*(x*y))",2);
gr->SubPlot(2,2,2); gr->Rotate(60,40);
gr->Alpha(true);
gr->Surf(a1); gr->Box();
Note, that it may entail a confusion. However, if one will use density plot then the picture will look better:
gr->SubPlot(2,2,3); gr->Rotate(60,40);
gr->Dens(a1); gr->Box();
return 0;
}
Note, that the previous color scheme is used in last plots because there are no direct specification of the one.
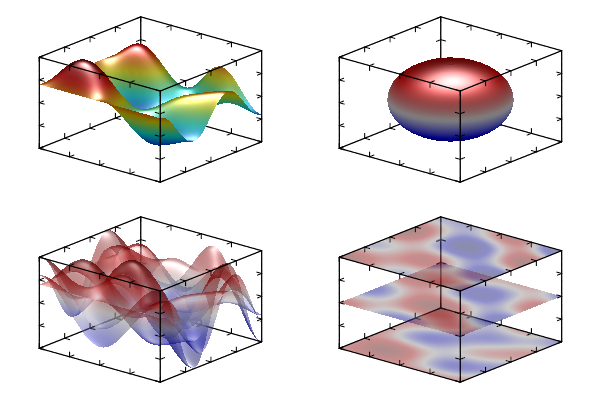
Example of surface plot for 2D data
Drawing of other 2D plots is analogous. The only peculiarity is the usage of flag ‘#’. By default this flag switches on the drawing of a grid on plot (Grid() or Mesh() for plots in plain or in volume). However, for isosurfaces (including surfaces of rotation Axial()) this flag switches the face drawing off. Figure becomes wired. The following code gives example of flag ‘#’ using (compare with normal function drawing as in its description):
int sample(mglGraph *gr, void *)
{
gr->Alpha(true); gr->Light(true); gr->Light(0,mglPoint(0,0,1));
mglData a(30,20);
a.Modify("0.6*sin(2*pi*x)*sin(3*pi*y) + 0.4*cos(3*pi*(x*y))");
gr->SubPlot(2,2,0); gr->Rotate(40,60);
gr->Surf(a,"BbcyrR#"); gr->Box();
gr->SubPlot(2,2,1); gr->Rotate(40,60);
gr->Dens(a,"BbcyrR#"); gr->Box();
gr->SubPlot(2,2,2); gr->Rotate(40,60);
gr->Cont(a,"BbcyrR#"); gr->Box();
gr->SubPlot(2,2,3); gr->Rotate(40,60);
gr->Axial(a,"BbcyrR#"); gr->Box();
return 0;
}
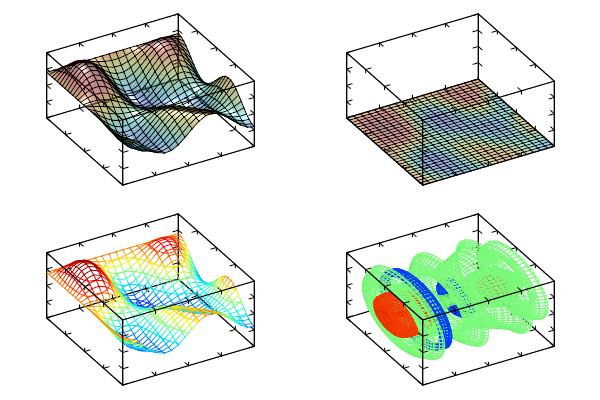
Example of 2D data plot with color scheme contained ‘#’ symbol
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
Drawing procedures for 3D plot looks similarly to 1D and 2D plots described above. There are 3 general types of 3D plots (see section 3D plotting): (i) plots on slices or on projections, (ii) isosurfaces, (iii) cloud-like plots. Plots on slice are clear enough – one specifies a slice (as its index or as coordinate value) and MathGL draws contour lines or density plot on slice plane. Isosurface gives more information. Isosurface is 3D analogue of the contour line Cont(). It shows the region where data array values exceed specified isosurface level. Plot becomes more informative if one adds transparency, lightning or sets color scheme depending on coordinates. Generalization of isosurface is the cloud-like plot. For this plot the darker color and less transparent regions correspond to higher values of data. Contrary, the regions with low values are transparent. For plotting of the phase of fields (or beams or pulses) one can use isosurface which transparency depends on the other data array (see function Surf3A()). As example of 3D data plots let us draw the Gaussian beam diffraction in space. Beam propagates along x axis:
int sample(mglGraph *gr, void *)
{
gr->Alpha(true); gr->Light(true);
gr->Light(0,mglPoint(0,0,1));
mglData a(30,30,30),b(30,30,30);
a.Modify("exp(-16*((z-0.5)^2+(y-0.5)^2)/(1+4*x^2))");
b.Modify("16*((z-0.5)^2+(y-0.5)^2)*(x)/(1+4*x^2)");
gr->CAxis(0,1);
gr->SubPlot(2,2,0); gr->Rotate(40,60);
gr->Surf3(a,"wgk"); gr->Box();
gr->SubPlot(2,2,1); gr->Rotate(40,60);
gr->DensA(a); gr->Box(); gr->Axis();
gr->SubPlot(2,2,2); gr->Rotate(40,60);
gr->CloudQ(a); gr->Box();
gr->SubPlot(2,2,3); gr->Rotate(40,60);
gr->Surf3A(b,a,"q");gr->Box();
return 0;
}

Example of Gaussian beam diffraction (3D data)
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
MathGL library has advanced features for setting and handling the surface transparency. The simplest way to add transparency is the using of function Alpha(). As a result, all further surfaces (and isosurfaces, density plots and so on) become transparent. However, their look can be additionally improved.
First, the selected surface will be non-transparent if one sets the flag Transparent before the surface drawing and sets it off after the drawing.
Second, the value of transparency can be different from surface to surface. To do it just change the value of AlphaDef before the drawing of the selected surface. If its value is close to 0 then the surface becomes more and more transparent. Contrary, if its value is close to 1 then the surface becomes practically non-transparent. This is some analogue of Transparent=true.
Third feature is the changing of the way how the light goes through overlapped surfaces. The variable TranspType defines it. By default the usual transparency is used (TranspType=0) – surfaces below is less visible than the upper ones. A “glass-like” transparency (TranspType=1) has a different look when the surface just decreases the background light (the surfaces are commutable in this case).
A “neon-like” transparency (TranspType=2) has more interesting look. In this case a surface is the light source (like a lamp on the dark background) and just adds some intensity to the color. At this, the library sets automatically the black color for the background and changes the default line color to white.
As example I shall show the variant of plot from Plots for 2D data (grid drawing is disabled) for different types of transparency.

Example of TranspType=0.

Example of TranspType=1.
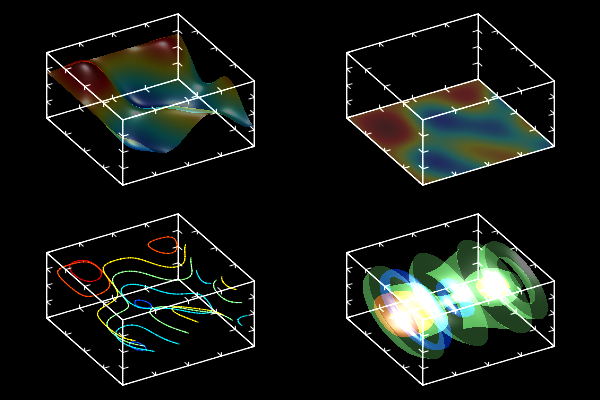
Example of TranspType=2.
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
The usage of pure C or Fortran or any similar interfaces (see section C interface) is practically identical to classes usage. But there are some differences. C functions must have argument HMGL (for graphics) and/or HMDT (for data arrays) which specifies the object for drawing or manipulating (changing). Fortran users may regard these variables as integer. So, firstly the user has to create this object by function mgl_create_*() and has to delete it after the using by function mgl_delete_*().
Also, all arguments of C function have to be defined. So there are several functions with practically identical names doing practically the same. But some of them have simplified interface for the quick plotting and some of them have access to all plotting parameters for manual tunning.
As an example of C function usage let me draw the plot from Plots for 2D data. The C code which does it is shown below:
#include <mgl/mgl_c.h>
int main()
{
HMGL gr = mgl_create_graph_zb(600, 400);
mgl_set_alpha(gr, true);
mgl_set_light(gr, true);
HMDT a = mgl_create_data_size(30,20,1);
mgl_data_modify(a,"0.6*sin(2*pi*x)*sin(3*pi*y) + 0.4*cos(3*pi*(x*y))",0);
mgl_subplot(gr, 2,2,0);
mgl_rotate(gr, 40,60,0);
mgl_surf(gr,a,"BbcyrR#");
mgl_box(gr, true);
mgl_subplot(gr, 2,2,1);
mgl_rotate(gr, 40,60,0);
mgl_dens(gr,a,"BbcyrR#",NAN);
mgl_box(gr, true);
mgl_subplot(gr, 2,2,2);
mgl_rotate(gr, 40,60,0);
mgl_cont(gr,a,"BbcyrR#",7,NAN);
mgl_box(gr, true);
mgl_subplot(gr, 2,2,3);
mgl_rotate(gr, 40,60,0);
mgl_axial(gr,a,"BbcyrR#",3);
mgl_box(gr, true);
/* don't forgot to save graphics */
mgl_write_png(gr,"sample.png",0);
return 0;
}
Practically the same simple to create a window. For example let rewrite the code from for window creation (see section Using FLTK/Qt/GLUT window):
int sample(HMGL gr, void *)
{
mgl_rotate(gr,60,40,0);
mgl_box(gr,1);
return 0;
}
//-----------------------------------------------------
int main(int argc,char **argv)
{
mgl_create_graph_fltk(sample, "MathGL examples", NULL);
mgl_fltk_run();
return 0;
}
The Fortran code have some peculiarities. Exactly it not allow one to send arbitrary parameter (which was NULL in previous example) to function. This is limitation of Fortran language. So, the corresponding code will be NOT TESTED NOW!!!:
program TEST
integer x,f,func
call mgl_create_graph_fltk(sample, 'MathGL examples');
call mgl_fltk_run();
end program TEST
integer function sample(gr)
integer*8 gr
call mgl_rotate(gr,60,40,0);
call mgl_box(gr,1);
sample=0
return
end
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
Generally SWIG based classes (including the Python one) are the same as C++ classes. However, there are few tips for using MathGL with PyQt. Below I place a very simple python code which demonstrate how MathGL can be used with PyQt. This code is mostly written by Prof. Dr. Heino Falcke. You can just copy it to a file mgl-pyqt-test.py and execute it from python shell by command execfile("mgl-pyqt-test.py")
from PyQt4 import QtGui,QtCore
from mathgl import *
import sys
app = QtGui.QApplication(sys.argv)
qpointf=QtCore.QPointF()
class hfQtPlot(QtGui.QWidget):
def __init__(self, parent=None):
QtGui.QWidget.__init__(self, parent)
self.img=(QtGui.QImage())
def setgraph(self,gr):
self.buffer='\t'
self.buffer=self.buffer.expandtabs(4*gr.GetWidth()*gr.GetHeight())
gr.GetBGRN(self.buffer,len(self.buffer))
self.img=QtGui.QImage(self.buffer, gr.GetWidth(),gr.GetHeight(),QtGui.QImage.Format_ARGB32)
self.update()
def paintEvent(self, event):
paint = QtGui.QPainter()
paint.begin(self)
paint.drawImage(qpointf,self.img)
paint.end()
BackgroundColor=[1.0,1.0,1.0]
size=100
gr=mglGraph()
y=mglData(size)
#y.Modify("((0.7*cos(2*pi*(x+.2)*500)+0.3)*(rnd*0.5+0.5)+362.135+10000.)")
y.Modify("(cos(2*pi*x*10)+1.1)*1000.*rnd-501")
x=mglData(size)
x.Modify("x^2");
def plotpanel(gr,x,y,n):
gr.SubPlot(2,2,n)
gr.SetXRange(x)
gr.SetYRange(y)
gr.AdjustTicks()
gr.Axis()
gr.Box()
gr.Label("x","x-Axis",1)
gr.Label("y","y-Axis",1)
gr.ClearLegend()
gr.AddLegend("Legend: "+str(n),"k")
gr.Legend()
gr.Plot(x,y)
gr.Clf(BackgroundColor[0],BackgroundColor[1],BackgroundColor[2])
gr.SetPlotFactor(1.5)
plotpanel(gr,x,y,0)
y.Modify("(cos(2*pi*x*10)+1.1)*1000.*rnd-501")
plotpanel(gr,x,y,1)
y.Modify("(cos(2*pi*x*10)+1.1)*1000.*rnd-501")
plotpanel(gr,x,y,2)
y.Modify("(cos(2*pi*x*10)+1.1)*1000.*rnd-501")
plotpanel(gr,x,y,3)
gr.WritePNG("test.png","Test Plot")
qw = hfQtPlot()
qw.show()
qw.setgraph(gr)
qw.raise_()
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
In this section I have included some small hints and advices for the improving of the quality of plots and for the demonstration of some non-trivial features of MathGL library. In contrast to previous examples I showed mostly the idea but not the whole drawing function. More examples with the source code can be find at http://mathgl.sf.net/ or in section Samples.
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
As I noted above, MathGL functions (except the special one, like Clf()) do not erase the previous plotting but just add the new one. It allows one to draw “compound” plots easily. For example, popular Matlab command surfc can be emulated in MathGL by 2 calls:
Surf(a);
Cont(a, 0, 7, -1); // draw contours at z = -1
Here a is 2-dimensional data for the plotting, -1 is the value of z-coordinate at which the contour should be plotted (at the bottom in this example). Analogously, one can draw density plot instead of contour lines and so on.
Another nice plot is contour lines plotted directly on the surface:
Light(true); // switch on light for the surface
Surf(a, "BbcyrR"); // select 'jet' colormap for the surface
Cont(a, "y"); // and yellow color for contours
The possible difficulties arise in black&white case, when the color of the surface can be close to the color of a contour line. In that case I may suggest the following code:
Light(true); // switch on light for the surface
Surf(a, "kw"); // select 'gray' colormap for the surface
CAxis(-1,0); // first draw for darker surface colors
Cont(a, "w"); // white contours
CAxis(0,1); // now draw for brighter surface colors
Cont(a, "k"); // black contours
CAxis(-1,1); // return color range to original state
The idea is to divide the color range on 2 parts (dark and bright) and to select the contrasting color for contour lines for each of part.
Similarly, one can plot flow thread over density plot of vector field amplitude (this is another amusing plot from Matlab) and so on. The list of compound graphics can be prolonged but I hope that the general idea is clear.
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
Developing the previous hint one can make a plot with 2 or more axes. The idea is that the change of settings does not influence on the already drawn graphics. So, for 2-axes plot let us set the first axis and draw everything concerning it. Then let us setup the second axis and draw things for the second axis. The corresponding code is (see section 2-axes sample):
// set up first axis
Axis(mglPoint(-1,-1,-1),mglPoint(1,1,1),mglPoint(-1,-1,-1));
Axis(); // draw it
Plot(y1,"b"); // draw something in first axis
// set up second axis
Axis(mglPoint(0,0,0),mglPoint(1,1,1),mglPoint(1,1,1));
Axis(); // draw it
Stem(y2,"r"); // draw something in second axis
Note, that the first and the second axes look better if being placed in different corners. In the code presented above the first axis is placed in the left-bottom corner, and the second one is placed in the right-top corner.
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
The printing of nice titles for the plot is not so trivial task in general case. The problem is that the rotation and aspect change lead to different looks for titles of different subplots. So, the resulting look is not so good as it could be. The solution is simple – to print titles exactly after SubPlot() call and before any rotation, aspect change and so on! Analogously, the title for the whole picture looks better if it is printed first (before any SubPlot() calls). Alternatively you can use function Title() for plotting title for the picture at any time.
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
By default (for the user comfort), the color range is set equal to z-range of the plot. However, there are different ranges. So, one can obtain amusing plot by the change of color range manually. For example, there are plots with one-color bottom (or top) or practically bi-color picture and so on.
For example, compare 2 surfaces:
SubPlot(2,1,0)
Surf(a); // usual coloring range
SubPlot(2,1,1)
CAxis(0,1);
Surf(a); // bottom of the surface have one-colour filling
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
Sometimes an experimental or numerical surface has outstanding points. Visualization of such surface will lead to the hole(s) in place of such points. The standard method of “fighting” – to change data values – is not always good and is not so convenient. MathGL library has another method – to set variable Cut=false. As a consequence, all outstanding points will be projected on the bounding box.
Such method is good not only for outstanding points but also for the case when one need to plane the bottom or the top of the plot. Exactly such case is demonstrated in the code:
mglData a(20,30); // create some data
a.Modify("0.6*sin(2*pi*x)*sin(3*pi*y) + 0.4*cos(3*pi*(x*y))");
// set lower border above the data minimal value
Axis(mglPoint(-1,-1,0),mglPoint(1,1,1));
Cut = false; // set off cutting flag
` Surf(a); // and draw the surface
It is an interesting result, is not it?
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
Vector field visualization (especially in 3d case Vect3 or VectC) may look tangly – there are too many overlapping lines. I may suggest 2 ways to solve this problem. The first one is to change MeshNum for decreasing the number of hachures. The second way is to use the flow thread chart Flow. Unfortunately, I don’t know any other methods to visualize 3d vector field. If you know any, e-mail me and I shall add it to MatGL.
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
In contrast to the most of other programs, MathGL supports several (up to 10) light sources. Moreover, the color each of them can be different: white (this is usual), yellow, red, cyan, green and so on. The use of several light sources may be interesting for the highlighting of some peculiarities of the plot or just to make an amusing picture. Note, each light source can be switched on/off individually (see section Several light sample).
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
MathGL library has a feature for cutting of points in some region CutMin*CutMax. Such an excision can be used to improve the look of the graphics. Moreover, this cutting may help to show an internal structure of an object (like isocaps plot in Matlab). For example, let us use the standard 3D data array and show its interior (see section CutMinMax sample).
mglData c(61,51,40); // create the data
mglData v(10); v.Fill(-0.5,1);
c.Modify("(-2*((2*x-1)^2 + (2*y-1)^2 + (2*z-1)^4 - (2*z-1)^2 - 0.1))");
gr->CutMin = mglPoint(0,-1,-1); gr->CutMax = mglPoint(1,0,1.1);
gr->Surf3(-0.5,c,"BbcyrR");
gr->ContF3(v,c,'x',-1,"BbcyrR"); gr->ContF3(v,c,'y',-1,"BbcyrR");
gr->ContF3(v,c,'z',0,"BbcyrR"); gr->ContF3(v,c,'z',39,"BbcyrR");
One can also exclude points from arbitrary area in space. This area defined by textual formula CutOff() (see section Cutting). The algorithm is the same as shown for “rectangular cutting”.
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
Sometime ago I worked with mapping and have a question about its visualization. Let me remember you that mapping is some transformation rule for one set of number to another one. The 1d mapping is just an ordinary function – it takes a number and transforms it to another one. The 2d mapping (which I used) is a pair of functions which take 2 numbers and transform them to another 2 ones. Except general plots (like SurfC, SurfA) there is a special plot – Arnold diagram. It shows the area which is the result of mapping of some initial area (usually square).
I tried to make such plot in Map. It shows the set of points or set of faces, which final position is the result of mapping. At this, the color gives information about their initial position and the height describes Jacobian value of the transformation. Unfortunately, it looks good only for the simplest mapping but for the real multivalent quasi-chaotic mapping it produces a confusion. So, use it if you like :).
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
Log-scaled plot can be drawn by 2 steps. First, one should change the scale of axis by call SetFunc("lg(x)", "lg(y)"); (in this example, x- and y-axis will be log-scaled). Second, one should set logarithmic scale for axis ticks by changing variables: SetTicks('x',0); SetTicks('y',0);. Finally, one should check (or change) the axis ranges and origin so that their values to be positive. For example of log-log plot see section Log-log sample.
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
As I have noted before, the change of settings will influence only for the further plotting commands. This allows one to create template function which will contain settings and primitive drawing for often used plots. Correspondingly one may call this template-function for drawing simplification.
For example, let one has a set of points (experimental or numerical) and wants to compare it with theoretical law (for example, with exponent law \exp(-x/2), x \in [0, 20]). The template-function for this task is:
void template(mglGraph *gr)
{
mglData law(100); // create the law
law.Modify("exp(-10*x)");
gr->Axis(mglPoint(0,0.0001), mglPoint(20,1), mglPoint(0,0.0001));
gr->SetFunc(0,"lg(y)",0); gr->dy = 0;
gr->Plot(law,"r2");
gr->Text(mglPoint(10,0.2),"Theoretical law: e^x","rL");
gr->Label('x',"x val."); gr->Label('y',"y val.");
gr->Axis(); gr->Grid("xy","g;"); gr->Box();
}
At this, one will only write a few lines for data drawing:
template(gr); // apply settings and default drawing from template
mglData dat("fname.dat"); // load the data
// and draw it (suppose that data file have 2 columns)
gr->Plot(dat.SubData(0),dat.SubData(1),"bx ");
A template-function can also contain settings for font, transparency, lightning, color scheme and so on.
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
Nonlinear fitting is rather simple. All that you need is the data to fit, the approximation formula and the list of coefficients to fit (better with its initial guess values). Let me demonstrate it on the following simple example (see section Fitting sample). First, let us use sin function with some random noise:
mglData rnd(100), idl(50); //data to be fitted and ideal data
rnd.Modify("0.4*rnd+0.1+sin(4*pi*x)");
idl.Modify("0.3+sin(4*pi*x)");
and plot it to see that data we will fit
gr->Axis(mglPoint(-1,-2), mglPoint(1,2));
gr->Plot(rnd, ". "); gr->Plot(idl, "b");
gr->Box();
gr->Text(mglPoint(0,2.2), "initial: y = 0.3+sin(2\pi x)", "C:b", -1);
The next step is the fitting itself. For that let me specify an initial values ini for coefficients ‘abc’ and do the fitting for approximation formula ‘a+b*sin(c*x)’
mglData res; // The data for found formula
float ini[3] = {1, 1, 3};
gr->Fit(res, rnd, "a+b*sin(c*x)", "abc", ini);
Now display it
gr->Plot(res, "r");
gr->Text(mglPoint(-1,-1.3), "fitted:", "L:r", -1);
gr->PutsFit(mglPoint(0,-1.8), "y = ", "C:r", -1);
NOTE! the fitting results may have strong dependence on initial values for coefficients due to algorithm features. The problem is that in general case there are several local "optimums" for coefficients and the program returns only first found one! There are no guaranties that it will be the best. Try for example to set ini[3] = {0, 0, 0} in the code above.
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
Solving of Partial Differential Equations (PDE, including beam tracing) and ray tracing (or finding particle trajectory) are more or less common task. So, MathGL have several functions for that. There are mglRay() for ray tracing, mglPDE() for PDE solving, mglQO2d() for beam tracing in 2D case (see section Global functions). Note, that these functions take “Hamiltonian” or equations as string values. And I don’t plan now to allow one to use user-defined functions. There are 2 reasons: the complexity of corresponding interface; and the basic nature of used methods which are good for samples but may not good for serious scientific calculations.
The ray tracing can be done by mglRay() function. Really ray tracing equation is Hamiltonian equation for 3D space. So, the function can be also used for finding a particle trajectory (i.e. solve Hamiltonian ODE) for 1D, 2D or 3D cases. The function have a set of arguments. First of all, it is Hamiltonian which defined the media (or the equation) you are planning to use. The Hamiltonian is defined by string which may depend on coordinates ‘x’, ‘y’, ‘z’, time ‘t’ (for particle dynamics) and momentums ‘p’=p_x, ‘q’=p_y, ‘v’=p_z. Next, you have to define the initial conditions for coordinates and momentums at ‘t’=0 and set the integrations step (default is 0.1) and its duration (default is 10). The Runge-Kutta method of 4-th order is used for integration.
mglData r,a,re(128),im(128);
r = mglRay("p^2+q^2-x-1", mglPoint(-0.7, -1), mglPoint(0, 0.5));
gr->Plot(r.SubData(0), r.SubData(1));
This example calculate the reflection from linear layer (media with Hamiltonian ‘p^2+q^2-x-1’=p_x^2+p_y^2-x-1). This is parabolic curve. The resulting array have 7 columns which contain data for {x,y,z,p,q,v,t}.
The solution of PDE is a bit more complicated. As previous you have to specify the equation as pseudo-differential operator \hat H(x, \nabla) which is called sometime as “Hamiltonian” (for example, in beam tracing). As previously, it is defined by string which may depend on coordinates ‘x’, ‘y’, ‘z’ (but not time!), momentums ‘p’=(d/dx)/i k_0, ‘q’=(d/dy)/i k_0 and field amplitude ‘u’=|u|. The evolutionary coordinate is ‘z’ in all cases. So that, the equation look like du/dz = ik_0 H(x,y,\hat p, \hat q, |u|)[u]. Dependence on field amplitude ‘u’=|u| allows one to solve nonlinear problems too. For example, for nonlinear Shrodinger equation you may set ham="p^2 + q^2 - u^2". Also you may specify imaginary part for wave absorption, like ham = "p^2 + i*x*(x>0)", but only if dependence on variable ‘i’ is linear (i.e. H = Hre+i*Him).
Next step is specifing the initial conditions at ‘z’=Min.z. The function need 2 arrays for real and for imaginary part. Note, that coordinates x,y,z are supposed to be in specified range [Min, Max]. So, the data arrays should have corresponding scales. Finally, you may set the integration step and paramter k0=k_0. Also keep in mind, that internally the 2 times large box is used (for suppressing numerical reflection from boundaries) and the equation should well defined even in this extended range.
Final comment is concerning the possible form of pseudo-differential operator H. At this moment, simplified form of operator H is supported – all “mixed” terms (like ‘x*p’->x*d/dx) are excluded. For example, in 2D case this operator is effectively H = f(p,z) + g(x,z,u). However commutable combinations (like ‘x*q’->x*d/dy) are allowed for 3D case.
So, for example let solve the equation for beam deflected from linear layer and absorbed later. The operator will have the form ‘"p^2+q^2-x-1+i*0.5*(z+x)*(z>-x)"’ that correspond to equation ik_0 \partial_z u + \Delta u + x \cdot u + i (x+z)/2 \cdot u = 0. This is typical equation for Electron Cyclotron (EC) absorption in magnetized plasmas. For initial conditions let me select the beam with plane phase front exp(-48*(x+0.7)^2). The corresponding code looks like this (see section PDE sample):
mglData a,re(128),im(128);
re.Fill("exp(-48*(x+0.7)^2)", gr->Min, gr->Max);
a = mglPDE("p^2+q^2-x-1+i*0.5*(z+x)*(z>-x)", re, im,
gr->Min, gr->Max, 0.01, 30);
a.Transpose("yxz");
gr->CAxis(0, 1);
gr->Dens(a,"wyrRk");
The last example is example of beam tracing. Beam tracing equation is special kind of PDE equation written in coordinates accompanied to a ray. Generally this is the same parameters and limitation as for PDE solving but the coordinates are defined by the ray and by parameter of grid width w in direction transverse the ray. So, you don’t need to specify the range of coordinates. BUT there is limitation. The accompanied coordinates are well defined only for smooth enough rays, i.e. then the ray curvature K (which is defined as 1/K^2 = (|\ddot r|^2 |\dot r|^2 - (\ddot r, \dot r)^2)/|\dot r|^6) is much large then the grid width: K>>w. So, you may receive incorrect results if this condition will be broken.
You may use following code for obtaining the same solution as in previous example:
mglData r, xx, yy, a, im(128), re(128);
const char *ham = "p^2+q^2-x-1+i*0.5*(y+x)*(y>-x)";
r = mglRay(ham, mglPoint(-0.7, -1), mglPoint(0, 0.5), 0.02, 2);
// now start beam tracing
re.Fill("exp(-48*x^2)", gr->Min, gr->Max);
a = mglQO2d(ham, re, im, r, 1, 30, &xx, &yy);
gr->CAxis(0, 1);
gr->Dens(xx, yy, a, "wyrRk");
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
Sometimes you may prefer to use MGL scripts in yours code. It is simpler (especially in comparison with C/Fortran interfaces) and fast way to plot the data with annotations, labels and so on. Class mglParse (see section mglParse class parse MGL scripts in C++. It have also the corresponding interface for C/Fortran.
The key function here is mglParse::Parse() (or mgl_parse() for C/Fortran) which execute one command per string. At this the detailed information about the possible errors or warnings is passed as function value. Or you may execute the whole script as long string with lines separated by ‘\n’. Functions mglParse::Execute() and mgl_parse_text() perform it. Also you may set the values of paramters ‘$0’...‘$9’ for the script by functions mglParse::AddParam() or mgl_add_param(), allow/disable picture resizing, check “once” status and so on. The usage is rather stright-forward.
The only non-obvious thing is data transition between script and yours program. There are 2 stages: add or find variable; and set data to variable. In C++ you may use functions mglParse::AddVar() and mglParse::FindVar() which return pointer to mglVar structure. This structure contain data itself, the variable name and callback function which will be called if variable destroied. Last feature allows you to control the presence of the variable and, for example, close a window with data if this variable is destroyed. In C/Fortran the corresponding functions are mgl_add_var(), mgl_find_var(). But these functions return the data array only. Note, you must not delete or free the data obtained from these functions!
So, some simple example at the end. Here I define a data array, create variable, put data into it and plot it. The C++ code looks like this:
float a[100]; // let a_i = sin(4*pi*x), x=0...1
for(int i=0;i<100;i++) a[i]=sin(4*M_PI*i/99);
mglParse *parser = new mglParse;
mglData &d = (parser->AddVar("dat"))->d;
d.Set(a,100); // set data to variable
parser->Execute(gr, "plot dat; xrange 0 1\nbox\naxis");
// you may break script at any line do something
// and continue after that
parser->Execute(gr, "xlabel 'x'\nylabel 'y'");
// also you may use cycles or conditions in script
parser->Execute(gr, "for $0 -1 1 0.1\nline 0 0 -1 $0 'r'\nnext");
gr->WritePNG("test.png"); // don't forgot to save picture
The code in C/Fortran looks practically the same:
float a[100]; // let a_i = sin(4*pi*x), x=0...1
int i;
for(i=0;i<100;i++) a[i]=sin(4*M_PI*i/99);
HMPR parser = mgl_create_parser();
HMDT d = mgl_add_var(parser, "dat");
mgl_data_set_float(d,a,100,1,1); // set data to variable
mgl_parse_text(gr, parser, "plot dat; xrange 0 1\nbox\naxis");
// you may break script at any line do something
// and continue after that
mgl_parse_text(gr, parser, "xlabel 'x'\nylabel 'y'");
// also you may use cycles or conditions in script
mgl_parse_text(gr, parser, "for $0 -1 1 0.1\nline 0 0 -1 $0 'r'\nnext");
mgl_write_png(gr, "test.png", ""); // don't forgot to save picture
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
One can easily create stereo image in MathGL. Stereo image can be produced by making two subplots with slightly different rotation angles. The corresponding code looks like this (see section Stereo image sample):
gr->SubPlot(2,1,0); // left image
gr->Rotate(40,60+3);
// draw something here
gr->SubPlot(2,1,1); // right image
gr->Rotate(40,60-3);
// draw the same here
| [ << ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
This document was generated by Alexey Balakin on May 2, 2013 using texi2html 1.82.